
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Сызықтық гармоникалық осциллятор үшін координата операторының орташа мәні бірлігінде: 0
Сызық тық гармоникалық осциллятор ү шін координата операторының орташа мә ні бірлігінде: 0
Сызық тық гармоникалық осциллятордың кинетикалық энергиясының орташа мә ні 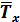 :
: 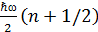
Сызық тық гармоникалық осциллятордың толқ ындық функциясының уақ ытқ а тә уелділігі  :
: 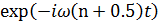
Тепе-тең бө лшектердің ұ қ састық принципі 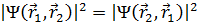
Тікбұ рышты ені шексіз жә не биіктігі  потенциалдық тосқ ауылғ а энергиясы
потенциалдық тосқ ауылғ а энергиясы 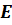 бө лшектер ағ ыны тү седі. Тосқ ауыл кең істікті екі
бө лшектер ағ ыны тү седі. Тосқ ауыл кең істікті екі 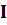 жә не
жә не 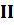 аймақ тарғ а бө леді, ондағ ы импульстер сә йкесінше
аймақ тарғ а бө леді, ондағ ы импульстер сә йкесінше 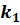 жә не
жә не 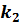 . Бө лшектердің тосқ ауылдан шағ ылу ық тималдығ ы:
. Бө лшектердің тосқ ауылдан шағ ылу ық тималдығ ы: 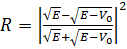 .
. 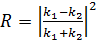
Тікбұ рышты ені шексіз жә не биіктігі  потенциалдық тосқ ауылғ а энергиясы
потенциалдық тосқ ауылғ а энергиясы 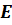 бө лшектер ағ ыны тү седі: x< 0 болғ анда V(x)=0, x≥ 0 болғ анда V(x)=0. I жә не II аймақ тарындағ ы толқ ындық сандары сә йкесінше анық талғ ан k1 жә не k2. Бірө лшемді
бө лшектер ағ ыны тү седі: x< 0 болғ анда V(x)=0, x≥ 0 болғ анда V(x)=0. I жә не II аймақ тарындағ ы толқ ындық сандары сә йкесінше анық талғ ан k1 жә не k2. Бірө лшемді 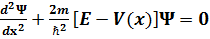 тең деунің шешімі:
тең деунің шешімі: 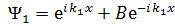 , I аймағ ында.
, I аймағ ында. 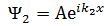 , II аймағ ында
, II аймағ ында
Тікбұ рышты, шексіз созылғ ан жә не биіктігі потенциалдық тосқ ауылғ а энергия ағ ынымен бө лшек келіп тү седі: V(x) = 0, x < 0 болғ анда (I) жә не V(x) = 0, x≥ 0 болады (II). I жә не II сә йкес аймақ та k1 жә не k2 толқ ын сандары анық талғ ан. Бірө лшемді тең деудің шешімі: и. Амплитудалары A жә не B: . . Кө ппе =азба??? А-В=1
Тікбұ рышты, шексіз созылғ ан жә не биіктігі  потенциалдық тосқ ауылғ а
потенциалдық тосқ ауылғ а 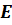 энергия ағ ынымен бө лшек келіп тү седі: V(x)=0, x< 0 болғ анда (I) жә не V(x)=0, x≥ 0 болады (II). I жә не II сә йкес аймақ та k1 жә не k2 толқ ын сандары анық талғ ан. Бірө лшемді тең деудің шешімі
энергия ағ ынымен бө лшек келіп тү седі: V(x)=0, x< 0 болғ анда (I) жә не V(x)=0, x≥ 0 болады (II). I жә не II сә йкес аймақ та k1 жә не k2 толқ ын сандары анық талғ ан. Бірө лшемді тең деудің шешімі 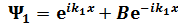 жә не
жә не 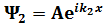 толқ ындардың жиынын сипаттайды:
толқ ындардың жиынын сипаттайды: 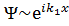 –тү скен,
–тү скен, 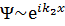 – ө ткен.
– ө ткен. 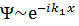 – шағ ылғ ан
– шағ ылғ ан
Толқ ындық функция квадратының 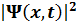 ө лшем бірлігі:
ө лшем бірлігі: 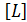 -1
-1
Толқ ындық функцияның квадраты 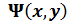 ө лшенеді
ө лшенеді 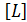 -1
-1
Толқ ындық функцияның нормалау шарты 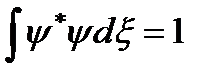 : энергияның сақ талу заң ымен біріктірілуі. нормалау сақ талу заң ының уақ ыт бойынша кө рінісі
: энергияның сақ талу заң ымен біріктірілуі. нормалау сақ талу заң ының уақ ыт бойынша кө рінісі
Толқ ындық функцияның шексіз терең тікбұ рышты бірө лшемді шұ ң қ ырының 2 тү йіні бар. Бұ л кү й n кванттық санғ а сә йкес келеді. 3
Толық уақ ыттық Шредингер тең деуінің анық тү рі. 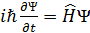
Туннельдік потенциальдық тосқ ауыл аймағ ының соң ғ ы ені (а – ені, 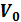 – тосқ ауыл биіктігі, m–бө лшек массасы,
– тосқ ауыл биіктігі, m–бө лшек массасы, 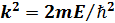 ,
, 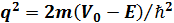 ), бө лшектің табылу ық тималдығ ы:
), бө лшектің табылу ық тималдығ ы: 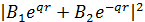
Туылу 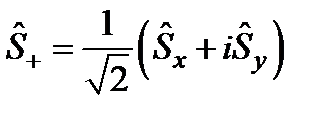 жә не жойылу
жә не жойылу 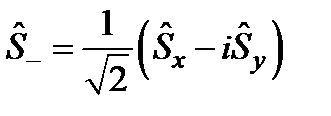 операторларының коммутациялық тең дігі:
операторларының коммутациялық тең дігі: 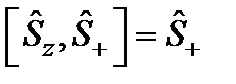 .
. 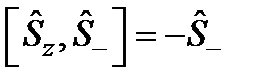 .
. 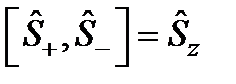 жә не
жә не 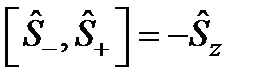
Ү шө лшемді гармоникалық осцилляторды кванттау ережесі: 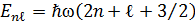
Шексіз биік жә не ені 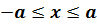 потенциалдық шұ ң қ ырдағ ы микробө лшектің орналасу ық тималдығ ы тығ ыздығ ының таралуы суретте келтірілген. Бұ л кү й: екі тармақ қ а ие. n = 3 кванттық санына сә йкес
потенциалдық шұ ң қ ырдағ ы микробө лшектің орналасу ық тималдығ ы тығ ыздығ ының таралуы суретте келтірілген. Бұ л кү й: екі тармақ қ а ие. n = 3 кванттық санына сә йкес
Шексіз биік потенциалдық шұ ң қ ырдағ ы микробө лшектің орналасу ық тималдығ ы тығ ыздығ ының таралуы суретте келтірілген. Бұ л кү й: екі тармақ қ а ие. 2-ші қ озғ ан кү йге сә йкес
Шексіз терең діктегі тік бұ рышты шұ ң қ ыр жә не соң ғ ы ендік 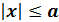 ү шін Шредингердің бірө лшемді тең деуі:
ү шін Шредингердің бірө лшемді тең деуі: 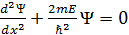
Шредингер тең деуін планетарлық жү йе есептеріне қ олдану мү мкіндігі: мү мкін емес
Шредингер тең деуінің стационар тү рі: 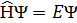
Шредингера тең деуіне кіретін y толқ ындық функциясы кө мегімен анық тауғ а болады: бө лшектің кең істіктің кез келген нү ктесінде орналасу ық тималдығ ын. физикалық шаманың орташа мә нін
Шредингердің стационарлық тең деуі келесі тү рге келтіріледі: 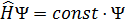
Шредингердің толқ ындық тең деуі: 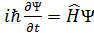
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|