
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Потенциал тосқауылына соңғы ені(а – ені, – тосқауыл биіктігі, m – бөлшек массасы, , ) бөлшек ағыны келіп түсті.
Потенциал тосқ ауылына соң ғ ы ені(а – ені, – тосқ ауыл биіктігі, m – бө лшек массасы, , ) бө лшек ағ ыны келіп тү сті.
Потенциалдық тосқ ауылғ а соң ғ ы ені(а – ені, 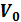 – тосқ ауыл биіктігі, m – бө лшек массасы,
– тосқ ауыл биіктігі, m – бө лшек массасы, 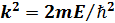 ,
, 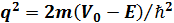 ) бө лшек ағ ыны келіп тү седі. Суреттегі II аймақ ү шін Шредингер тең деуі:
) бө лшек ағ ыны келіп тү седі. Суреттегі II аймақ ү шін Шредингер тең деуі: 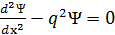
Потенциалдық шұ ң қ ырдың шексіз қ абырғ аларында бө лшек энергетикалық дең гейде квантталады, 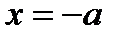 жә не
жә не 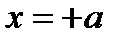 нү ктелерінде орналасқ ан, шартымен анық талады:
нү ктелерінде орналасқ ан, шартымен анық талады: 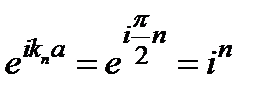 , мұ ндағ ы
, мұ ндағ ы 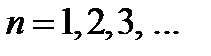 .
. 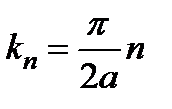 , мұ ндағ ы
, мұ ндағ ы 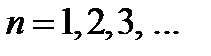
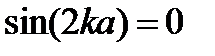
Проекция операторы кү йінен S = 0 кү йіне S = 1: 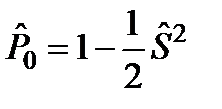 .
.  .
. 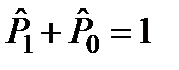
Свойства полиномов Эрмита: ортонормаланғ ан. жұ п. (ортагональдау, нормалау бө лшектеу)
Синглеттік жә не триплеттік кү йлерде проекция операторы S = 0 жә не S = 1: 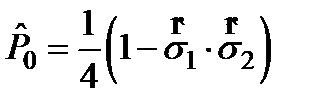 .
. 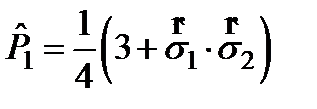 .
. 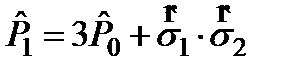
Сонымен тә жірибеден мынадай тұ жырым жасауғ а болады: электрон фермион болып табылады жә не параллель спин сияқ ты, z осімен антипараллель спинге де йе бола алады
Спектрі дискретті айнығ ан функция ү шін ортонормалау шарты: 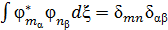
Спектрі ү здіксіз толқ ындық ф-ң нормалау ережесі: 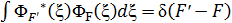
Стационар есептеулерде 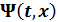 уақ ыттан тә уелділік:
уақ ыттан тә уелділік: 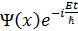
Стационар жү йелерде уақ ыттан тә уелді емес: гамильтон операторының орташа мә ндері. ық тималдық тығ ыздығ ы. операторлардың меншікті мә ндері...
стационар жү йелерде уақ ыттан тә уелді: еркін бө лшектің толқ ындық функциясы. дискретті айнымағ ан спекетрдің толқ ындық функциялары. айнығ ан спектр
Стационар кү йлерде: ық тималдық тығ ыздығ ы уақ ыттан тә уелді емес. толқ ындық функциялар уақ ыттан анық тә уелді
Стационар ө рістегі 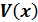 бө лшек ү шін мына тең дік орындалады:
бө лшек ү шін мына тең дік орындалады: 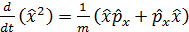
Суперпозиция принципі мынадай болжам жасайды: еғ ер жү йе 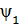 жә не
жә не 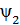 кү йлерінде бола алса, онда ол мына кү йде де бола алады
кү йлерінде бола алса, онда ол мына кү йде де бола алады 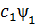 +
+ 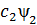
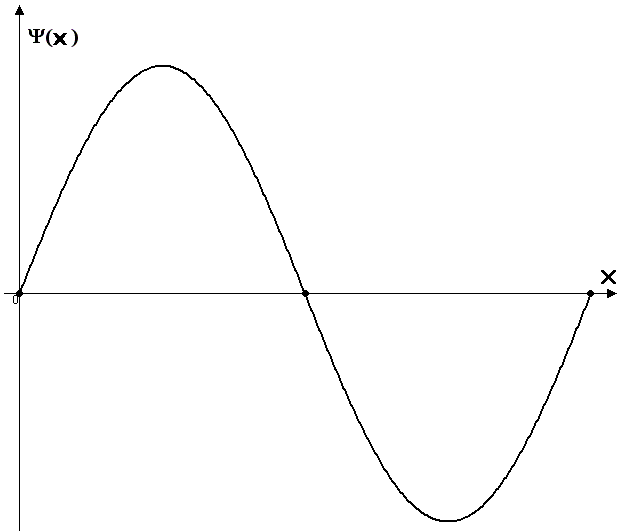 Суретте кө рсетілген толқ ындық функция шексіз терең потенциалдық шұ ң қ ырдағ ы микробө лшектің кү йін сипаттайды: 1-ші қ озғ ан кү йді
Суретте кө рсетілген толқ ындық функция шексіз терең потенциалдық шұ ң қ ырдағ ы микробө лшектің кү йін сипаттайды: 1-ші қ озғ ан кү йді
Суреттегі I аймақ ү шін Шредингер тең деуі: 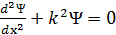
Сфералық айнымалыларда 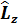 операторының комутаторы
операторының комутаторы 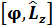 неге тең:
неге тең: 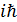
Сызық ты гармоникалық осцилятордың толқ ындық функциясының асимптотикасы 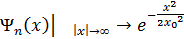
Сызық ты кез келген 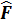 операторына келесі операторлардың эрмиті:
операторына келесі операторлардың эрмиті: 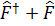 .
. 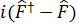
Сызық ты кез келген 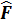 операторына келесі операторлардың эрмиті:
операторына келесі операторлардың эрмиті: 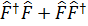 .
. 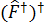 .
. 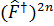
Сызық тық гармоникалық осциллятор ү шін координата операторының 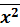 орташа мә ні
орташа мә ні 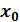 бірлігінде:
бірлігінде: 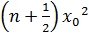
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|