
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Меншікті функция және меншікті мәнінің спин операторы
Меншікті функция 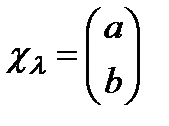 жә не меншікті мә нінің
жә не меншікті мә нінің 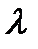 спин операторы
спин операторы 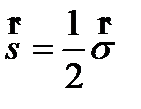 тең деуінен табылады
тең деуінен табылады 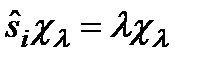 , где
, где 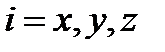 . М. ф. жә не м. м. операторы
. М. ф. жә не м. м. операторы 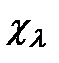 :
: 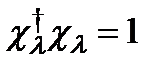 .
. 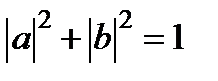
Меншікті функция 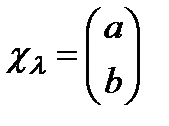 жә не меншікті мә нінің
жә не меншікті мә нінің 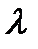 спин операторы
спин операторы 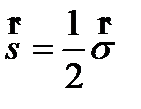 тең деуінен табылады
тең деуінен табылады 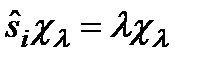 , мұ ндағ ы
, мұ ндағ ы 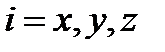 . М. ф. жә не м. м. операторы
. М. ф. жә не м. м. операторы 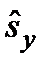 :
: 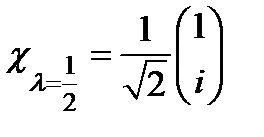 .
. 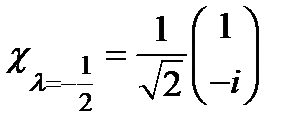 .
. 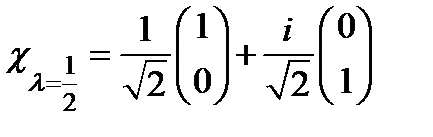
Меншікті функция 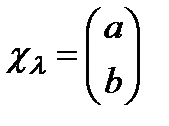 жә не меншікті мә нінің
жә не меншікті мә нінің 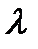 спин операторы
спин операторы 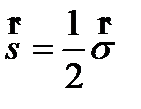 тең деуінен табылады
тең деуінен табылады 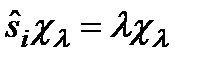 , мұ ндағ ы
, мұ ндағ ы 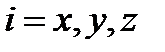 . М. ф. жә не м. м. операторы
. М. ф. жә не м. м. операторы 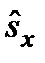 :
: 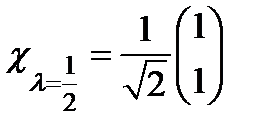 .
. 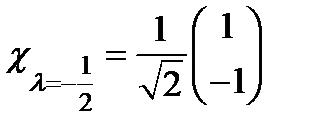 .
. 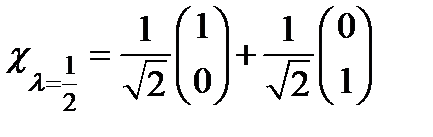
Меншікті функцияларының ортақ жү йесі жоқ операторлардың жұ бы: 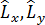
Микрожү йелер 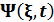 толқ ындық функциямен сипатталады деген пікір –бұ л: Место для формулы. Постулат
толқ ындық функциямен сипатталады деген пікір –бұ л: Место для формулы. Постулат
Мына шарт орындалғ анда, операторымыз эрмитті болады: 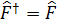 .
. 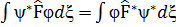
Нү ктелік зарядталғ ан бө лшектердің 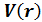 кулондық потенциалы тең:
кулондық потенциалы тең: 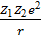
Операторларды квадраттағ андағ ы нә тиже: 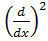 =
= 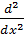 .
. 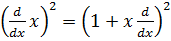 .
. 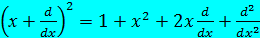
Операторлардың кө бейтіндісін уақ ыт бойынша дифференциалдау ережесі: 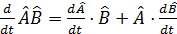
Операторлардың кө бейтіндісінің уақ ыт бойынша дифференциалдау ережесі: 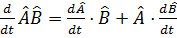
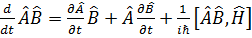
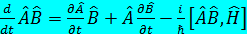
Орталық симметриялық потенциалда энергетикалық спектрлер азғ ындалуының ең кіші бө лгіші: 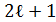 m магниттік кванттық сан бойынша
m магниттік кванттық сан бойынша
Орталық -симметриялық ө рісте 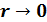 болғ анда радиальды толқ ындық функцияның кө рінісі
болғ анда радиальды толқ ындық функцияның кө рінісі 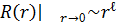
Ө лшеп отырғ ан шамамыз 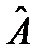 анық талғ ан болып табылатын шарт:
анық талғ ан болып табылатын шарт: 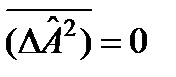 .
. 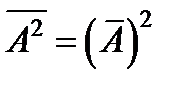 .
. 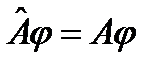
Ө ткізбейтін екі қ абырғ аларының арасында бө лшек бар, 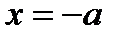 жә не
жә не 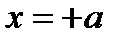 нү ктелерінде орналасқ ан. Стационарлық кү й ү шін
нү ктелерінде орналасқ ан. Стационарлық кү й ү шін 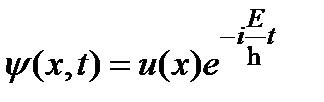 . Кең істік бө лігіндегі тең деу ү шін
. Кең істік бө лігіндегі тең деу ү шін 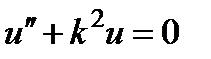 шешімге ие
шешімге ие 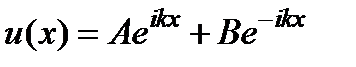 , мұ ндағ ы коэффициеттер
, мұ ндағ ы коэффициеттер 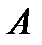 жә не
жә не  : шекаралық шарттан табылады
: шекаралық шарттан табылады 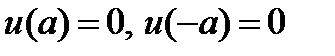 .
. 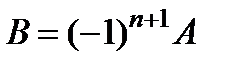 , мұ ндағ ы
, мұ ндағ ы 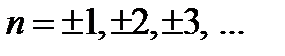
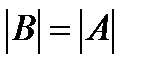 нормалау шартынан табылады
нормалау шартынан табылады 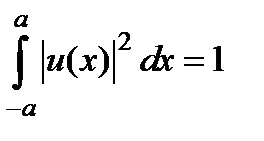
Паули матрицасының коммутациялық қ ұ рылымы: 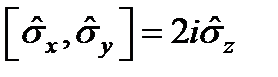 .
. 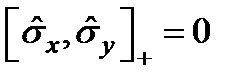
Паули матрицасының қ ұ рылымы: 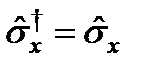 ,
, 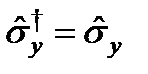 ,
,  – эрмитті.
– эрмитті. 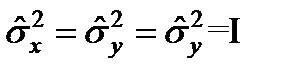 , мұ нда I – бірлік матрицасы.
, мұ нда I – бірлік матрицасы. 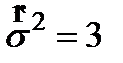
Паули мтрицасының кө бейтіндісі: 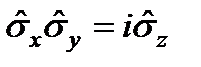 ,
, 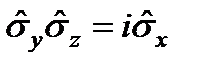 ,
, 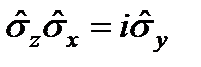 .
. 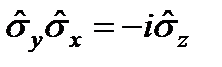 ,
, 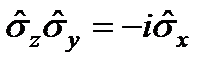 ,
, 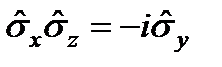 .
. 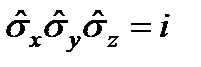 цикл бойынша т. б.
цикл бойынша т. б.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|