
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Кез келген оператор өзгермейді: комплексті түйіндеу еселігі кезінде. еселі транспонирлеу кезінде. еселі эрмитті түйіндес оператор
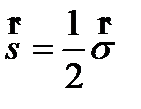 тең деуінен табылады
тең деуінен табылады 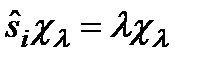 , мұ ндағ ы
, мұ ндағ ы 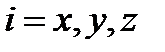 . М. ф. жә не м. м. операторы
. М. ф. жә не м. м. операторы 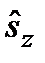 :
: 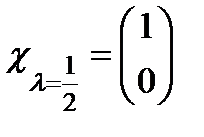 .
. 
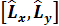 Коммутаторы тең:
Коммутаторы тең: 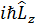
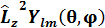 операторының квантталу ережесі:
операторының квантталу ережесі: 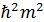
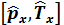 коммутаторы неге тең: 0
коммутаторы неге тең: 0
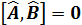 жә не
жә не 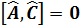 берілген,
берілген, 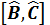 коммутаторы туралы не айтуғ а болады
коммутаторы туралы не айтуғ а болады 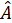 жә не
жә не 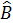 операторларының нақ ты мә ніне байланысты
операторларының нақ ты мә ніне байланысты
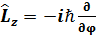 , операторының меншікті мә ні, егер меншікті функция
, операторының меншікті мә ні, егер меншікті функция 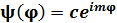 болса:
болса: 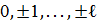
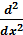 операторының меншікті функциясы:
операторының меншікті функциясы: 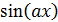
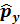 импульстың проекциясының операторы меншікті толқ ындық функцияғ а ие
импульстың проекциясының операторы меншікті толқ ындық функцияғ а ие 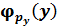 :
: 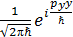
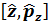 коммутаторы тең :
коммутаторы тең : 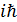
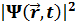 толқ ындық функцмясының квадраты ө лшенеді:
толқ ындық функцмясының квадраты ө лшенеді: 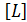 -3
-3
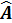 жә не
жә не 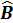 операторлары коммутацияланбайды,
операторлары коммутацияланбайды, 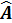 жә не
жә не 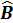 эрмитті опреаторлар.
эрмитті опреаторлар. 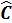 операторы эрмитті мына жағ дайда:
операторы эрмитті мына жағ дайда: 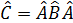
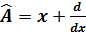 операторының меншікті функциялары
операторының меншікті функциялары 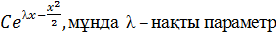
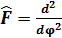 операторының меншікті мә ні, егер меншікті фун-я мынандай болса
операторының меншікті мә ні, егер меншікті фун-я мынандай болса 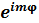 :
: 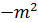
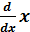 операторының эквиваленттік кө рінісі:
операторының эквиваленттік кө рінісі: 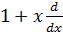
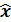 координата ү шін орта мә ннен ауытқ у операторының анық тамасы:
координата ү шін орта мә ннен ауытқ у операторының анық тамасы: 
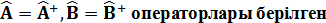 .
. 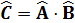 операторы мынадай қ асиетке йе:
операторы мынадай қ асиетке йе: 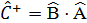
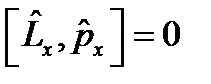 .
.  ,
, 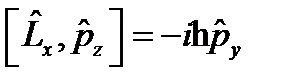
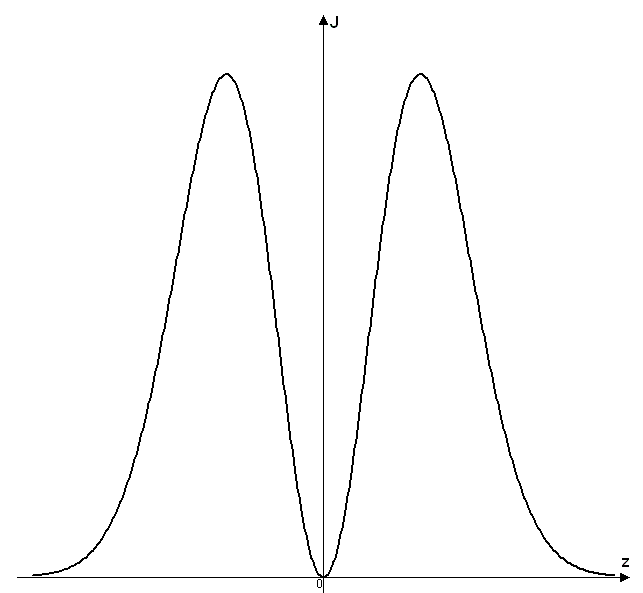
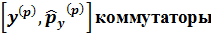 импульстік кө ріністе мынағ ан тең болады: iℏ
импульстік кө ріністе мынағ ан тең болады: iℏ 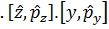
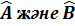 – эрмитті жә не коммутацияланбайды. Мына операторлардың комбинациясының эрмиті:
– эрмитті жә не коммутацияланбайды. Мына операторлардың комбинациясының эрмиті: 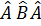 .
. 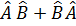 .
. 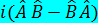
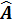 операторының меншікті функциялары
операторының меншікті функциялары 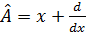 ,
, 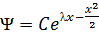 ,
, 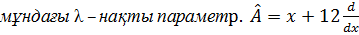 ,
, 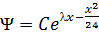 ,
, 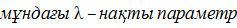
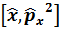 коммутаторы тең болады:
коммутаторы тең болады: 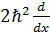 . 2i
. 2i 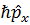
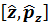 коммутаторытең болады:
коммутаторытең болады: 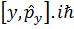
1927 жылы дә лелденген, Гейзенбергтің анық талмағ андық қ атынасы бойынша каноникалық тү йіндес шамалардың анық талмағ андығ ы арасында келесі байланыс болады: 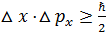 .
. 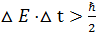
1927 жылы дә лелденген, Гейзенбергтің анық талмағ андық қ атынасы бойынша екі каноникалық тү йіндес айнымалылардың кө бейтіндісінің мә ні ћ реттен кем бола алмайды. ћ мә ні аз болғ андық тан (ћ=1, 05 10-34 Дж× с), анық талмағ андық қ атынас тек микроә лемде байқ алады
n=6 дең гейдегі сутек атомының азғ ындау еселігі 36
n=7 кү йдегі бірө лшемді осциллятордың толық энергиясы: 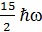
N-ө лшемді гармоникалық осциллятордың энергиясының квантталу ережесі. Еn тең: 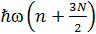
z осіне бұ раштық моменттің операторы: 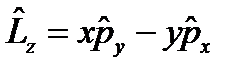 .
. 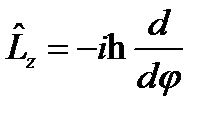 .
. 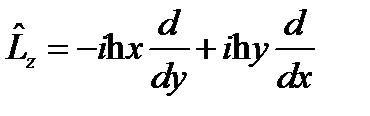
Аудару коэффициенті 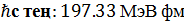
Бір экспериментте келесі шамаларды анық тауғ а болады: 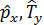

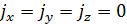
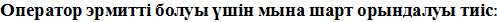
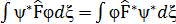
Бірө лшемді гармоникалық осциллятордың минималды энергиясы (n=0, 1, 2, 3, …): 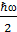
Бірө лшемді потенциал ү шін Гамильтон операторы 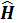 неге тең:
неге тең: 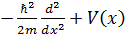
Бірө лшемді сызық тық гармоникалық осцилляторды кванттау ережесі: 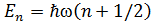
Бө лшек екі ө ткізбейтін қ абырғ алардың арасында периодтық қ озғ алыс жасайды, 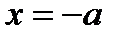 жә не
жә не 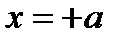 нү ктелерінде орналасқ ан. Стационарлық кү й ү шін
нү ктелерінде орналасқ ан. Стационарлық кү й ү шін 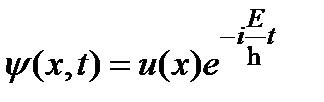 . Шредингер тең деуінің кең істіктік бө лігі ү шін
. Шредингер тең деуінің кең істіктік бө лігі ү шін 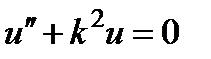 шешімге ие
шешімге ие 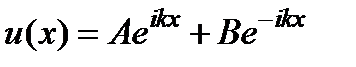 . Меншікті функцияның
. Меншікті функцияның 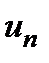 квантталуын толық тай анық тайтын шарт: шекаралық шарт
квантталуын толық тай анық тайтын шарт: шекаралық шарт 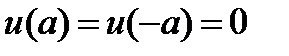 жә не нормалау шарты
жә не нормалау шарты 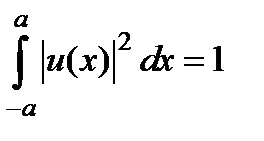 .
. 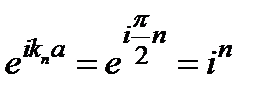 жә не
жә не 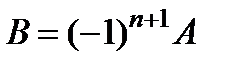 .
. 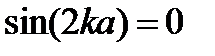 и
и 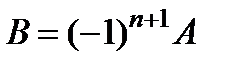
Бө лшек 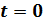 уақ ыт мезетінде бірінші қ озғ ан кү йде, гармоникалық осциллятор ө рісінде
уақ ыт мезетінде бірінші қ озғ ан кү йде, гармоникалық осциллятор ө рісінде 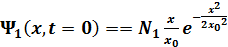 орналасқ ан. t> 0 уақ ыт мезетінде ол мына кү йде орналасады:
орналасқ ан. t> 0 уақ ыт мезетінде ол мына кү йде орналасады: 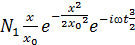
Бө лшектерді алмастыру операторының 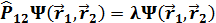 меншікті мә ні
меншікті мә ні 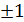
Бө лщек гармоникалық осциллятор ө рісінде бірінші қ озғ ан кү йде орналасқ ан 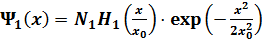 . Осы кү йдегі импульстің орташа мә ні:
. Осы кү йдегі импульстің орташа мә ні: 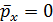
Бұ л кү йдегі импльстің орта мә ні қ андай 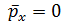
Бұ раштық момент операторының компоненті 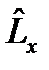 ,
, 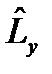 и
и 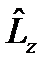 : ө зара коммутацияланбайды. операторымен коммутацияланады
: ө зара коммутацияланбайды. операторымен коммутацияланады 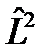 . эрмитті
. эрмитті 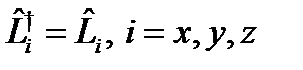
Бұ раштық моменттің компоненті ү шін коммутациялық тең дік: 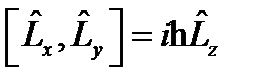 жә не цикл бойынша
жә не цикл бойынша 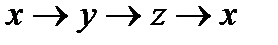 жә не т. б.
жә не т. б. 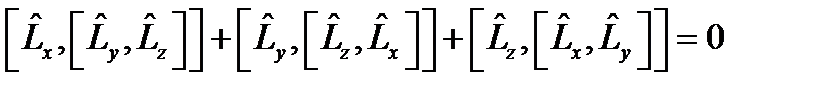
Бұ рыштық момент операторының компоненті 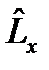 жә не импульс проекциясы операторларының комутаторлары:
жә не импульс проекциясы операторларының комутаторлары:
Бұ рыштық момент операторының компоненті 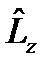 жә не импульс проекциясы операторларының комутаторлары:
жә не импульс проекциясы операторларының комутаторлары: 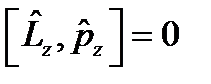 .
. 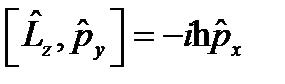 ,
, 
Бұ рыштық момент операторының компоненті 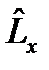 жә не координат операторларының комутаторлары:
жә не координат операторларының комутаторлары: 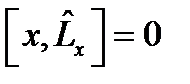 .
. 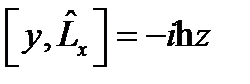 ,
, 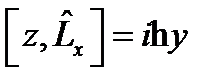
Бұ рыштық момент операторының компоненті 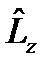 жә не координат операторларының комутаторлары:
жә не координат операторларының комутаторлары: 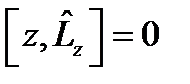 .
. 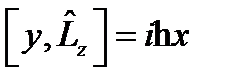 ,
, 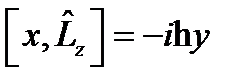
Гармоникалық осциллятордың сызық ты потенциалы: 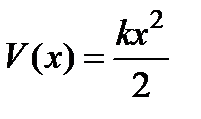 , мұ ндағ ы
, мұ ндағ ы 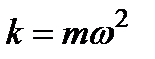 .
. 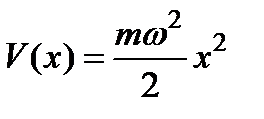
Гармоникалық осциллятордың толқ ындық функциясының асимптотикалық тү рі  :
: 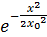
Гейзенбергтің анық талмағ андық принципіне бағ ынатын шамалар: 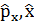
Дискретті айнымағ ан спектр жағ дайы ү шін толқ ындық функцияның толық тық шарты: 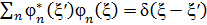
Егер 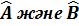 – коммутацияланады, онда келесі операторларды мынадай тү рде елестетеміз:
– коммутацияланады, онда келесі операторларды мынадай тү рде елестетеміз: 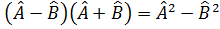 .
. 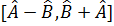 =0.
=0. 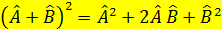
Егер 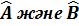 – коммутацияланбайды, онда келесі операторларды мынадай тү рде елестетеміз:
– коммутацияланбайды, онда келесі операторларды мынадай тү рде елестетеміз: 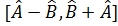 =2
=2  .
. 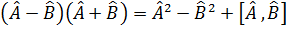 .
. 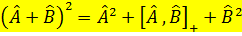 OK!!
OK!!
Егер 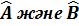 – эрмитті жә не коммутацияланбайды, онда келесі оператор
– эрмитті жә не коммутацияланбайды, онда келесі оператор 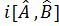 – эрмитті.
– эрмитті. 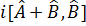 – эрмитті.
– эрмитті. 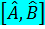 – эрмитті емес
– эрмитті емес
Егер 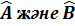 – эрмитті жә не коммутацияланбайды, онда келесі операторлардың эрмиті:
– эрмитті жә не коммутацияланбайды, онда келесі операторлардың эрмиті: 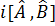 .
. 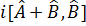
Егер бө дшектер жылдамдығ ы бірдей болса, ең ү лкен де Бройль толқ ын ұ зындығ ына ие болады: электрон. позитрон
Егер бө лшектердің де Бройльдік толқ ын ұ зындық тары бірдей болса, ең ү лкен жылдамдық қ а ие болады:
Егер екі кванто-механикалық шамалар коммутацияланса, онда: ортақ меншікті функциялар жү йесіне ие жә не бір экспериментте ө лшеуге болады
Егер екі оператор коммутацияланбаса, олар: Анық талмағ андық принципіне бағ ынады
Егер екі оператор коммутацияланса, онда: оларда меншікті функциялардың ортақ жү йесі болады. олардың орташаларын бір тә жірибеде ө лшеуге болады. (толық жинқ қ а кіреді)
Егер екі оператор коммутацияланса, олар: Меншікті функцияларының ортақ жү йесі бар
Екі оператор коммутацияланады, егер 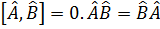
Екі оператор коммутацияланса, 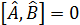
Екіө лшемді гармоникалық осциллятордың нолдік энергиясы 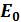 неге тең:
неге тең: 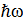
Ені шектеулі потелциалдық тосқ ауылғ а (а – ені,  – тосқ ауыл биіктігі, m – бө лшекмассасы)бө лшектер ағ ыны тү седі. Суреттегі IIаймағ ы ү шін Шредингер тең деуі мына тү рде болады:
– тосқ ауыл биіктігі, m – бө лшекмассасы)бө лшектер ағ ыны тү седі. Суреттегі IIаймағ ы ү шін Шредингер тең деуі мына тү рде болады: 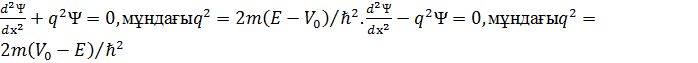
Еркін бө лшек yz жазық тығ ында қ озғ алады. Бө лшектің 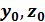 нү ктесінде табылу ық тималдығ ы
нү ктесінде табылу ық тималдығ ы 
Еркін бө лшек ү шін 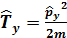 операторының меншікті мә ні:
операторының меншікті мә ні: 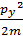
Еркін бө лшек ү шін 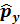 операторының меншікті мә ні:
операторының меншікті мә ні: 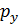
Еркін бө лшектің стационар Шредингер тең деуінің уақ ыттан тә уелділігі: 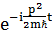
Ә серлесу орталық -симметриялық деп аталады, егер потенциал функциямен берілсе: 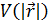
Импульстық кө ріністегі 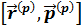 коммутаторы тең:
коммутаторы тең: 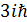
Импульстық кө ріністегі импульс операторы 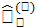 :
: 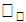
импульстық кө ріністегі 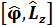 коммутаторы неге тең
коммутаторы неге тең 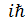
Импульстық кө ріністегі коммутатор 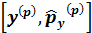 :
: 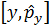
Импульстық кө ріністегі сызық тық гармоникалық осциллятор ү шін Шредингер тең деуі: 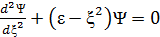
Импульстық кө ріністегі сызық тық гармоникалық осциллятордың энергетикалық спектрін 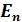 кванттау ережесі
кванттау ережесі 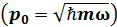 :
: 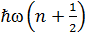
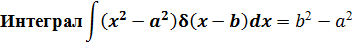
Интерпретация шарты 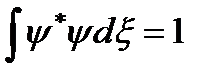 : толқ ындық функцияның дискретті спектрін нормалау шарты. заттың сақ талу заң ы. бө лшектің
: толқ ындық функцияның дискретті спектрін нормалау шарты. заттың сақ талу заң ы. бө лшектің 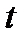 сә т уақ ытындағ ы
сә т уақ ытындағ ы 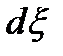 кө лемде энергияның сақ талу заң ымен біріктірілуіндегі табылу ық тималдылығ ы
кө лемде энергияның сақ талу заң ымен біріктірілуіндегі табылу ық тималдылығ ы
Каноникалық тү йіндес шамалар болып табылатындар: (x, px), (y, py), (z, pz), (E, t)
Кванто-механикалық жү йенің толқ ындық функциясы жалпы жағ дайда келесі айнымалыларғ а тә уелді: ξ – жалпы координата, t – уақ ыттық айнымалы
Квантомеханикалық шама қ озғ алыс интегралы болып табылады, егер: 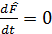
Кванто-механикалық шамаларды уақ ыт бойынша дифференциалдау ережесі: 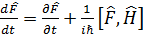
Кванттық механикада 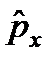 импульс проекция операторының дисперсиясы:
импульс проекция операторының дисперсиясы: 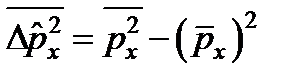 .
. 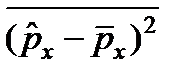 .
. 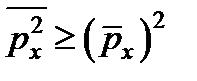
Кванттық механикада оператордың орта мә ні ө лшенетін шама болып табылады. Математикалық анық тама берініз 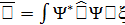
Кванттық механикада дисперсия 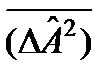 :
: 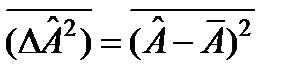 .
. 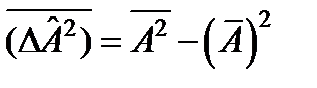 . қ алыпты анық талғ ан болып табылады
. қ алыпты анық талғ ан болып табылады
Кванттық механикада 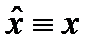 координат операторының дисперсиясы:
координат операторының дисперсиясы: 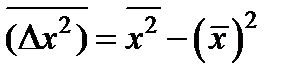 .
. 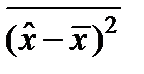 .
. 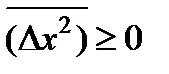 немесе
немесе 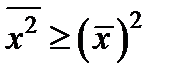
Кванттық механикада ү здіксіз тең деуі 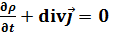 (
( 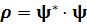 – ық тимал тығ ыздығ ы
– ық тимал тығ ыздығ ы 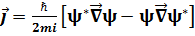 – ток тығ ыздығ ының ық тималдығ ы) сақ талу заң ын кө рсетеді: ық тималдылық. бө лшектің саны
– ток тығ ыздығ ының ық тималдығ ы) сақ талу заң ын кө рсетеді: ық тималдылық. бө лшектің саны
Кванттық механикадағ ы коммутатор – бұ л: 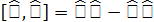
Кванттық -механикалық шама қ озғ алыс интегралы болады, егер: 
Кванттық -механикалық шамаларды уақ ыт бойынша диффернциалдау ережесі: 
Кез келген оператор ө згермейді: комплексті тү йіндеу еселігі кезінде. еселі транспонирлеу кезінде. еселі эрмитті тү йіндес оператор
Кез келген ү ш сызық ты оператор Якоби тепе-тең дігін қ анағ аттандырады: 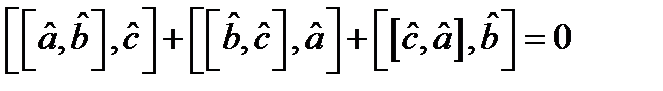 .
. 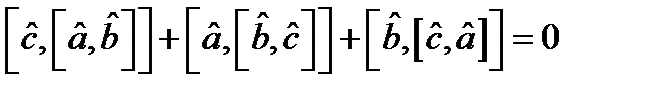
Келесі операторлардың жұ бының меншікті функцияларының ортақ жү йесі жоқ. 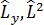
Коммутатор 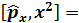 , егер Якоби тең дігі орындалса
, егер Якоби тең дігі орындалса 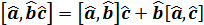 :
: 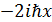
Коммутатор 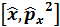 неге тең: 2i
неге тең: 2i 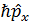
Коммутатор 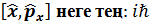
Электрондардың суық эмиссия механизмі негізделген: туннельдік эффектке
Коммутатор 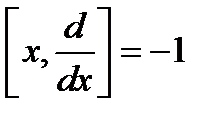 . Коммутаторлар:
. Коммутаторлар: 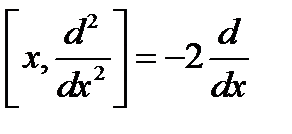 .
. 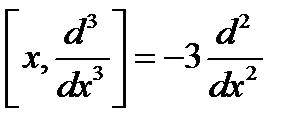 .
. 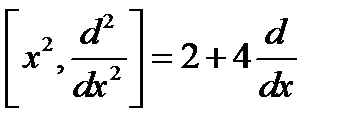
Координат операторының импульстық кө ріністегі мә ні 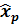 :
: 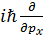
Координаттық кө ріністегі гармоникалық осциллятор ү шін бірө лшемді Шредингер тең деуі, мұ нда 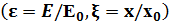 ,
, 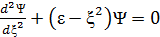
Мезосутектің бор орбитасы (mπ =273mе, сутек атомының бор орбитасы 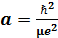 ): ~
): ~ 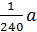
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|