
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Индивидуальные задания к контрольной работе №11 4 страница
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 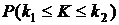 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 6; b) n=50, p=0, 01; c) n=400, p=0, 9, 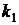 =350,
=350, 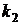 =365.
=365.
7. Плотность распределения 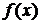 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 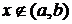
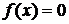 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 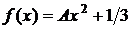 ,
,  =(0; 1),
=(0; 1),  =
= 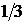 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 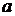 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 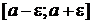 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 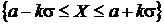 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 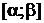 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 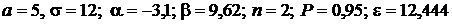 .
.
Вариант №18.
1. Сколькими способами из колоды, имеющей 36 карт, можно выбрать 4 карты так, что среди них окажется один туз?
2. В лифт 7-этажного дома на первом этаже вошли 6 пассажиров. Какова вероятность того, что четверо выйдут на одном этаже, если каждый из пассажиров с одинаковой вероятностью выходит на любом из этажей, начиная со второго?
3. Из пяти деталей выбирают одну годную, проверяя их последовательно. Каждая из деталей имеет дефект с вероятностью 0, 2. Найти вероятность того, что годная деталь нашлась раньше, чем проверили все детали.
4. Транзистор принадлежит к одной из трех партий с вероятностями 0, 25; 0, 5 и 0, 25. Вероятность того, что транзистор проработает заданное число часов, для этих партий равна соответственно 0, 8; 0, 8 и 0, 6. Определить вероятность того, что транзистор проработает заданное число часов. Какова вероятность того, что проработавший заданное число часов транзистор принадлежит второй партии?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 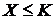 при следующих условиях. В партии из 15 деталей 10 деталей первого сорта, остальные второго. Отобраны случайным образом 4 детали. Х – число деталей второго сорта среди отобранных,
при следующих условиях. В партии из 15 деталей 10 деталей первого сорта, остальные второго. Отобраны случайным образом 4 детали. Х – число деталей второго сорта среди отобранных, 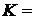 3.
3.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 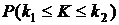 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=4, p=0, 5; b) n=200, p=0, 0085; c) n=900, p=0, 2, 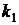 =170,
=170, 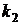 =200.
=200.
7. Плотность распределения 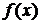 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 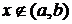
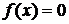 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 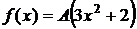 ,
,  =(0; 1),
=(0; 1),  =
= 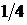 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 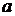 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 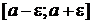 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 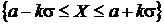 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 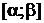 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 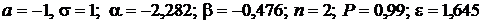
Вариант №19.
1. Из 10 теннисисток и 6 теннисистов составляются 4 смешанные пары. Сколькими способами это можно сделать?
2. В лотерее разыгрывается 6 ценных подарков. Найти вероятность того, что среди 4 наудачу взятых билетов окажется 2 " счастливых", если всего было выпущено 50 билетов.
3. Три стрелка производят по одному выстрелу по мишени. Вероятность попадания для первого стрелка 0, 5; для второго – 0, 8; для третьего – 0, 3. Найти вероятность, что в мишени будет две пробоины.
4. На сборку поступают детали с двух автоматов. Первый автомат дает 80%, остальные – второй. Первый автомат дает 1% брака, второй – 4%. Найти вероятность, что две проверенные детали окажутся бракованными. Определить вероятность того, что обе проверенные детали, оказавшиеся бракованными, изготовлены первым автоматом.
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 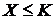 при следующих условиях. Трасса движения слаломиста состоит из четырех участков, каждый из которых он проходит с вероятностью 0, 8. В случае непрохождения одного из них спортсмен снимается с трассы. Х – число пройденных участков,
при следующих условиях. Трасса движения слаломиста состоит из четырех участков, каждый из которых он проходит с вероятностью 0, 8. В случае непрохождения одного из них спортсмен снимается с трассы. Х – число пройденных участков, 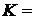 2.
2.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 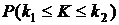 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=6, p=0, 25; b) n=150, p=0, 005; c) n=1350, p=0, 4, 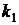 =500,
=500, 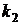 =550.
=550.
7. Плотность распределения 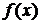 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 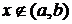
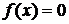 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 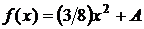 ,
,  =(0; 2),
=(0; 2),  =1.
=1.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 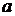 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 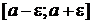 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 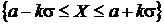 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 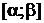 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 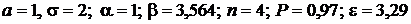
Вариант №20.
1. Сколькими способами можно распределить 30 различных предметов между тремя людьми так, чтобы каждый получил 10 предметов?
2. 8 вариантов контрольной работы, написанных каждый на отдельной карточке, перемешиваются и распределяются случайным образом среди 6 студентов, сидящих за круглым столом, причем каждый получает по одному варианту. Найти вероятность, что варианты 1 и 2 достанутся рядом сидящим.
3. Из колоды в 36 карт последовательно извлекают одну за другой три карты без возвращения. Найти вероятность того, что извлечено не более одного туза.
4. Из 20 стрелков 5 попадают в мишень с вероятностью 0, 8; 8 – с вероятностью 0, 7; 4 – с вероятностью 0, 6 и 3 – с вероятностью 0, 5. Наудачу выбранный стрелок произвел выстрел. Какова вероятность того, что он промахнется? Найти вероятность того, что выбран стрелок из группы пяти метких, если он промахнулся.
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 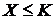 при следующих условиях. Бросаются 5 монет одновременно. Х – число выпавших " орлов",
при следующих условиях. Бросаются 5 монет одновременно. Х – число выпавших " орлов", 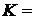 3.
3.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 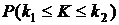 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=6, p=0, 75; b) n=60, p=0, 015; c) n=900, p=0, 1, 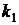 =75,
=75, 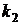 =100.
=100.
7. Плотность распределения 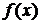 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 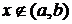
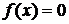 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 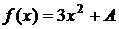 ,
,  =(0; 1),
=(0; 1),  =
= 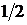 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 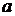 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 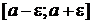 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 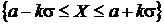 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 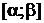 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 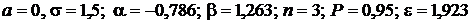 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|