
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Индивидуальные задания к контрольной работе №11 2 страница
Дано: a) n=5, p= 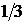 ; b) n=20, p=0, 02; c) n=600, p=0, 4,
; b) n=20, p=0, 02; c) n=600, p=0, 4, 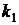 =250,
=250, 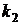 =330.
=330.
7. Плотность распределения 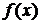 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 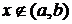
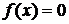 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 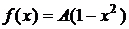 ,
,  =(0; 1),
=(0; 1),  =
= 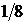 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 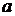 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 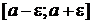 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 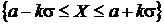 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 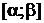 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 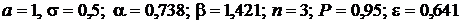 .
.
Вариант №7.
1. Из цифр 1, 2, 3, 4, 5 составляются пятизначные числа, не кратные пяти и не содержащие одинаковых цифр. Сколько существует таких чисел?
2. Ребенок, играя с карточками, на которых написаны буквы латинского алфавита (26 карточек), случайным образом выбирает 6 карточек. Найти вероятность того, что из букв, написанных на них, можно составить слово " BEGIN".
3. Из пяти ключей к замку подходит один. Ими пытаются открыть дверь, откладывая не подошедшие ключи в сторону. Найти вероятность, что для открытия двери потребуется не более трех попыток.
4. В цехе имеется три станка. Вероятность изготовления стандартной детали на первом станке составляет 0, 78, на втором – 0, 92, на третьем – 0, 86. Ввиду различного местоположения рабочий выбирает первый станок с вероятностью 0, 5; второй – 0, 2; третий – 0, 3. Найти вероятность, что изготовленная им на выбранном станке деталь окажется нестандартной. Какова вероятность того, что деталь изготавливалась на третьем станке, если она оказалась нестандартной?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 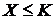 при следующих условиях. По мишени одновременно стреляют 3 стрелка, вероятности попаданий которых равны соответственно 0, 65; 0, 7 и 0, 8. Х – число попаданий,
при следующих условиях. По мишени одновременно стреляют 3 стрелка, вероятности попаданий которых равны соответственно 0, 65; 0, 7 и 0, 8. Х – число попаданий, 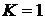 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 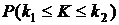 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=6, p=0, 1; b) n=600, p=0, 0025; c) n=768, p=0, 25, 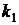 =190,
=190, 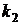 =220.
=220.
7. Плотность распределения 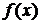 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 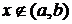
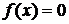 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 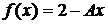 ,
,  =(0; 1),
=(0; 1),  =
= 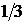 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 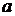 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 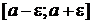 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 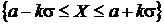 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 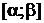 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 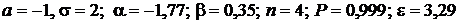 .
.
Вариант №8.
1. Сколькими способами можно расставить на шахматной доске 2 белых и 2 черных коня? Конь может стоять на любой клетке, а одноцветные фигуры неразличимы.
2. Найти вероятность того, что 7 случайно выбранных человек родились в разные дни недели.
3. Два стрелка стреляют по очереди, но не более трех раз каждый. Победителем считается тот, что первым попадет в мишень. При одном выстреле они попадают в мишень с вероятностью 0, 9 и 0, 8. Найти вероятность, что победит более меткий стрелок, если он начал стрелять первым.
4. По команде " огонь" одно из трех орудий стреляет по мишени. Вероятность попадания для орудий равна соответственно 0, 8; 0, 8; 0, 6. Команда " огонь" подается в 2 раза чаще первому орудию, чем второму и третьему по отдельности. Найти вероятность, что мишень окажется пораженной. Какова вероятность того, что мишень была поражена выстрелом из 3-го орудия?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 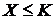 при следующих условиях. В темной комнате 7 красных кубиков и 8 синих, не отличимых друг от друга на ощупь. Мальчик вынес 3 кубика. Х – число красных кубиков среди вынесенных,
при следующих условиях. В темной комнате 7 красных кубиков и 8 синих, не отличимых друг от друга на ощупь. Мальчик вынес 3 кубика. Х – число красных кубиков среди вынесенных, 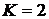 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 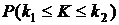 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=4, p=0, 4; b) n=50, p=0, 004; c) n=100, p=0, 9, 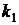 =85,
=85, 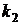 =92.
=92.
7. Плотность распределения 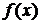 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 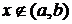
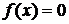 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 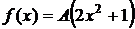 ,
,  =(0; 1),
=(0; 1),  =0, 1.
=0, 1.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 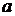 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 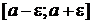 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 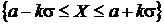 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 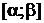 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 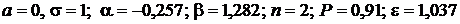 .
.
Вариант №9.
1. Среди 10 книг 7 книг различных авторов, и три книги одного автора. Сколькими способами можно расставить эти книги на полке так, чтобы книги одного автора стояли рядом?
2. Выполняя заказ на изготовление 50 золотых медалей, ювелир заменил 2 медали на фальшивые. Для контроля заказчик случайным образом выбирает три медали. Какова вероятность разоблачения ювелира?
3. В урне 6 белых и 8 черных шаров. Взято подряд без возвращения два шара. Найти вероятность, что они одного цвета.
4. В первой урне 3 белых и 2 черных шара; во второй – 3 белых и 5 черных. Из первой во вторую перекладывают, не глядя, два шара, после чего из второй урны извлекают шар. Найти вероятность того, что этот шар окажется белым. Какова вероятность того, что из первой урны во вторую были переложены белый и черный шары, если из второй урны извлечен белый шар?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 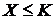 при следующих условиях. Производится набрасывание колец на колышек до первого успеха, при этом число всех колец, имеющихся в распоряжении, равно 5. Х – число использованных колец, вероятность набрасывания равна 0, 25;
при следующих условиях. Производится набрасывание колец на колышек до первого успеха, при этом число всех колец, имеющихся в распоряжении, равно 5. Х – число использованных колец, вероятность набрасывания равна 0, 25; 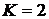 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 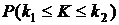 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=4, p= 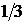 ; b) n=400, p=0, 0025; c) n=100, p=0, 8,
; b) n=400, p=0, 0025; c) n=100, p=0, 8, 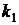 =75,
=75, 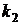 =84.
=84.
7. Плотность распределения 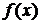 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 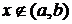
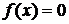 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 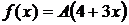 ,
,  =(0; 1),
=(0; 1),  =1.
=1.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 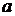 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 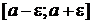 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 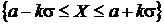 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 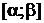 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 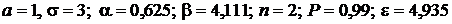 .
.
Вариант №10.
1. Сколькими способами можно расставить на 32 черных полях шахматной доски 12 белых и 12 черных шашек? На клетку ставится не более одной шашки.
2. Наудачу выбирается семизначное число. Найти вероятность того, что число одинаково читается как слева направо, так и справа налево (например, 4321234).
3. Рабочий обслуживает три станка, работающих независимо. Вероятность того, что в течение часа не потребует внимания рабочего: первый станок – 0, 9; второй – 0, 8; третий – 0, 85. Найти вероятность того, что в течение часа два станка потребуют внимания рабочего.
4. На сборку поступили транзисторы с двух заводов-изготовителей, причем первый завод поставил 30%, остальные – второй. Вероятность отказа для транзистора первого завода 0, 1, а второго – 0, 15. В блок поставлено два наудачу взятых транзистора. Найти вероятность, что блок неисправен. Какова вероятность, что оба транзистора изготовлены вторым заводом, если блок неисправен? Блок не работает, если дефект имеет хоть один транзистор.
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 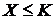 при следующих условиях. Производится выстрел из трех орудий одновременно по цели с вероятностями попадания 0, 5; 0, 6 и 0, 7 для каждого орудия. Х – число попаданий,
при следующих условиях. Производится выстрел из трех орудий одновременно по цели с вероятностями попадания 0, 5; 0, 6 и 0, 7 для каждого орудия. Х – число попаданий, 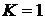 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 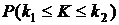 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 7; b) n=100, p=0, 007; c) n=150, p=0, 6, 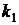 =86,
=86, 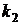 =96.
=96.
7. Плотность распределения 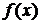 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 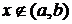
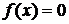 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 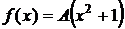 ,
,  =(0; 2),
=(0; 2),  =1.
=1.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 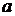 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 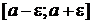 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 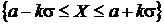 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 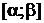 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 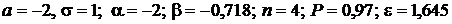 .
.
Вариант №11.
1. Тридцать человек разбиты на три группы по десять человек в каждой. Сколько может быть различных составов групп?
2. Рассеянная студентка написала письма 5 подругам, запечатала в конверты и обнаружила, что забыла написать адреса получателей. Какова вероятность того, что " свои" письма получат в точности три подруги, если адреса на конвертах будут написаны наудачу?
3. В урне 2 белых и 3 черных шара. Два игрока вынимают из урны поочередно шары, не возвращая их обратно. Выигрывает тот, кто раньше извлечет белый шар. Найти вероятность того, что выиграет начинающий.
4. Пятнадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся студент может ответить только на 25 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса из одного билета или на один вопрос из первого билета и на указанный дополнительный вопрос из другого билета. Какова вероятность того, что студент сдал экзамен, ответив на вопросы из одного билета?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 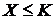 при следующих условиях. В урне 4 белых и 5 черных шаров. Наудачу один за другим из урны извлекаются шары до появления первого черного. Х – число оставшихся в урне белых шаров,
при следующих условиях. В урне 4 белых и 5 черных шаров. Наудачу один за другим из урны извлекаются шары до появления первого черного. Х – число оставшихся в урне белых шаров, 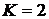 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 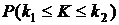 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 8; b) n=50, p=0, 002; c) n=192, p=0, 75, 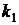 =230,
=230, 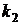 =150.
=150.
7. Плотность распределения 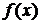 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 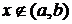
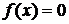 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 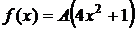 ,
,  =(0; 1),
=(0; 1),  =
= 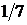 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 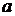 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 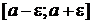 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 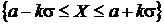 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 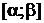 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|