
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Индивидуальные задания к контрольной работе №11 3 страница
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 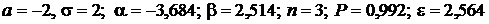 .
.
Вариант №12.
1. Из 12 разных книг 4 имеют переплет. Сколькими способами можно выбрать 5 книг так, что среди них 2 в переплете?
2. На столе экзаменатора – 25 занумерованных экзаменационных билетов. Два студента по очереди берут по одному билету. Найти вероятность того, что меньший номер у выбранных билетов равен 7.
3. Рабочий обслуживает 4 независимо работающих станка, которые в течение часа требуют его внимания с вероятностью 0, 1; 0, 1; 0, 2 и 0, 3 соответственно. Какова вероятность, что в течение часа не более одного станка потребуют его внимания?
4. На общий конвейер поступают узлы, изготовленные двумя рабочими. Производительность второго рабочего вдвое больше, чем первого. Вероятность допустить брак для первого рабочего 0, 075, а для второго 0, 09. Найти вероятность, что поступивший на общий конвейер узел будет иметь брак. Какова вероятность, что узел, оказавшийся бракованным, изготовлен вторым рабочим?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 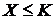 при следующих условиях. Некто забыл последнюю цифру шифра кодового замка. Зная, что это одна из цифр 5, 6, 7, 8, 9, он случайным образом их перебирает. Х – число попыток,
при следующих условиях. Некто забыл последнюю цифру шифра кодового замка. Зная, что это одна из цифр 5, 6, 7, 8, 9, он случайным образом их перебирает. Х – число попыток, 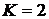 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 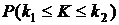 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=4, p=0, 1; b) n=40, p=0, 001; c) n=100, p=0, 1, 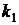 =8,
=8, 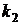 =20.
=20.
7. Плотность распределения 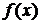 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 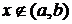
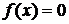 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 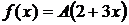 ,
,  =(0; 1),
=(0; 1),  =
= 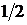 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 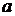 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 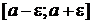 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 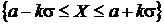 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 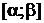 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 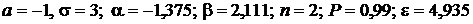 .
.
Вариант №13.
1. Тренер по фигурному катанию принял в секцию 6 мальчиков и 6 девочек. Сколькими способами он может сформировать смешанные пары?
2. Ребенок, играя с карточками, на которых написаны буквы латинского алфавита (26 букв), случайным образом выбирает 4 карточки. Какова вероятность того, что из букв, написанных на них, можно составить слово " READ"?
3. Три стрелка выстрелили по мишени по одному разу. Вероятность попадания для них 0, 9; 0, 8 и 0, 7 соответственно. Найти вероятность, что мишень поражена не более одного раза.
4. Покупатель приобрел электролампочку. Известно, что в момент покупки партия лампочек содержала 60% продукции местного предприятия и 40% – иногороднего. 500 часов работают безотказно каждые 90 из 100 лампочек местного завода и 80 из 100 иногороднего. Найти вероятность, что купленная лампочка проработает 500 часов. Какова вероятность того, что лампочка, проработавшая 500 часов безотказно, местного производства?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 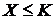 при следующих условиях. Вероятность попадания в цель из орудия при первом выстреле равна 0, 3; при втором – 0, 4; при третьем – 0, 5; при четвертом – 0, 9. Стрельба ведется до первого попадания, но не свыше 4 выстрелов. Х – число произведенных выстрелов,
при следующих условиях. Вероятность попадания в цель из орудия при первом выстреле равна 0, 3; при втором – 0, 4; при третьем – 0, 5; при четвертом – 0, 9. Стрельба ведется до первого попадания, но не свыше 4 выстрелов. Х – число произведенных выстрелов, 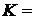 3.
3.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 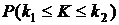 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 3; b) n=500, p=0, 003; c) n=400, p=0, 8, 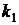 =300,
=300, 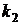 =330.
=330.
7. Плотность распределения 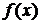 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 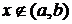
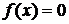 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 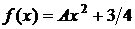 ,
,  =(0; 1),
=(0; 1),  =
= 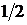 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 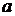 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 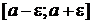 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 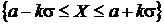 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 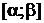 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 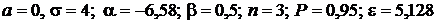 .
.
Вариант №14.
1. Лифт отправился с четырьмя пассажирами и останавливается далее на восьми этажах. Сколькими способами пассажиры могут выйти из лифта?
2. Каждый из 5 шаров случайным образом кладут в один из 6 ящиков. Какова вероятность, что все шары попадут в разные ящики?
3. Стрелок имеет 6 патронов. При одном выстреле он попадает в мишень с вероятностью 0, 7. Найти вероятность, что для поражения мишени ему потребуется не более половины патронов.
4. Узлы поступают на общий конвейер с двух участков. Вероятность брака узла с первого участка составляет 0, 05, со второго – 0, 10. Второй участок имеет производительность в 1, 5 раза больше, чем первый. Найти вероятность того, что взятый с конвейера узел окажется годным. Какова вероятность того, что годный узел изготовлен на первом участке?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 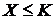 при следующих условиях. В партии из 10 деталей содержится 7 деталей первого сорта. Случайным образом одну за другой без возвращений извлекаем детали до появления детали первого сорта. Х – число попыток,
при следующих условиях. В партии из 10 деталей содержится 7 деталей первого сорта. Случайным образом одну за другой без возвращений извлекаем детали до появления детали первого сорта. Х – число попыток, 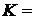 2.
2.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 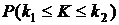 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 08; b) n=500, p=0, 004; c) n=600, p=0, 6, 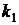 =340,
=340, 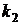 =380.
=380.
7. Плотность распределения 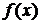 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 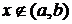
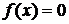 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 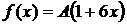 ,
,  =(0; 1),
=(0; 1),  =
= 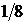 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 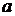 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 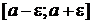 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 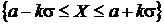 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 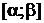 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 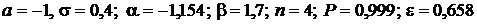 .
.
Вариант №15.
1. Пять групп занимаются в пяти расположенных подряд аудиториях. Сколько существует вариантов расписания, при которых группы №1 и №2 находились бы в соседних аудиториях?
2. У радиомонтажника имеется 20 микросхем, из них пятнадцать выпущены в мае, а пять – в июне. Радиомонтажник наугад выбирает 10 микросхем и устанавливает в прибор. Найти вероятность того, что в приборе окажется 6 микросхем, выпущенных в мае, и 4 – в июне.
3. Прибор состоит из трех элементов. Отказы элементов за некоторое время 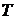 независимы, а их вероятности равны соответственно 0, 1; 0, 2 и 0, 25. Найти вероятность, что за время
независимы, а их вероятности равны соответственно 0, 1; 0, 2 и 0, 25. Найти вероятность, что за время 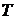 откажут два элемента.
откажут два элемента.
4. Из урны, содержащей 3 белых и 2 черных шара, переложено 2 шара в урну, содержащую 4 белых и 4 черных шара. Вычислить вероятность вынуть белый шар из второй урны. Какова вероятность, что из первой урны во вторую урну было переложено 2 черных шара, если извлеченный наудачу шар из второй урны оказался белым?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 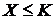 при следующих условиях. По мишени ведется стрельба до первого попадания, но не более 4 раз. Вероятность попадания при каждом выстреле 0, 9. Х – число выстрелов,
при следующих условиях. По мишени ведется стрельба до первого попадания, но не более 4 раз. Вероятность попадания при каждом выстреле 0, 9. Х – число выстрелов, 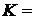 2.
2.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 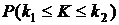 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=6, p=0, 3; b) n=60, p=0, 01; c) n=768, p=0, 75, 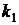 =580,
=580, 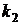 =610.
=610.
7. Плотность распределения 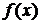 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 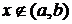
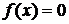 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 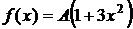 ,
,  =(0; 1),
=(0; 1),  =
= 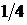 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 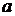 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 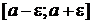 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 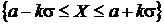 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 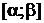 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 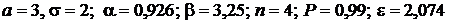 .
.
Вариант №16.
1. На грядке растет 9 белых и 6 красных роз. Сколькими способами из них можно выбрать для букета 3 белые и 2 красные розы?
2. 10 человек входят в комнату, где имеется всего 8 стульев, и рассаживаются случайным образом, но так, что все стулья оказываются занятыми. Какова вероятность того, что два определенных человека останутся без места?
3. В урне 5 белых и 4 черных шара. Из урны наугад один за другим без возвращения извлекают шары. Найти вероятность того, что второй по порядку шар будет белым.
4. Первое орудие батареи из четырех орудий пристреляно так, что вероятность попадания равна 0, 4. Остальные три орудия попадают с вероятностью 0, 2. Для поражения цели достаточно одного попадания. Два орудия произвели по одному выстрелу. Найти вероятность поражения цели. Какова вероятность того, что первое орудие стреляло, если цель оказалась пораженной?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 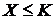 при следующих условиях. Вероятность попадания в цель из орудия при первом выстреле равна 0, 1; при втором 0, 3; при третьем 0, 5; при четвертом 0, 8. Производится четыре выстрела. Х – число попаданий в цель,
при следующих условиях. Вероятность попадания в цель из орудия при первом выстреле равна 0, 1; при втором 0, 3; при третьем 0, 5; при четвертом 0, 8. Производится четыре выстрела. Х – число попаданий в цель, 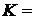 1.
1.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 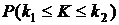 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 1; b) n=60, p=0, 02; c) n=400, p=0, 1, 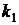 =35,
=35, 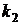 =50.
=50.
7. Плотность распределения 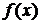 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 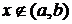
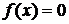 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 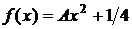 ,
,  =(0; 2),
=(0; 2),  =
= 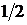 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 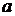 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 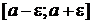 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 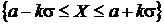 ;
;
3) найти вероятность попадания n случайно выбранных деталей в интервал 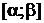 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 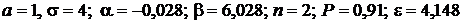 .
.
Вариант №17.
1. В поход на неделю собирается 8 человек. Сколькими способами они могут составить расписание дежурств, если каждый будет дежурить не более одного дня и дежурство длится полный день?
2. Среди кандидатов в сборную команду института 3 первокурсника, 4 второкурсника и 7 третьекурсников. Для участия в соревнованиях формируется сборная из 5 человек. Какова вероятность того, что в сборной не окажется второкурсников, если отбор в сборную производится случайным образом?
3. Электрическая цепь составлена по схеме (рис. 3). Элементы цепи
выходят из строя с вероятностью 0, 1; 0, 3; 0, 1; 0, 2 соответственно. Найти вероятность того, что цепь работает.
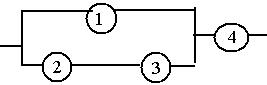
Рис. 3
4. Для сигнализации о неполадке в работе автоматической линии используется один индикатор, принадлежащий с вероятностями 0, 2; 0, 3 и 0, 5 к одному из трех типов, для которых вероятности срабатывания при нарушении нормальной работы линии равны соответственно 1, 99; 0, 75 и 0, 40. Найти вероятность, что индикатор срабатывает при неполадке в работе линии. Какова вероятность, что для контроля используется индикатор 1-го типа, если он подал сигнал о произошедшей в работе линии неполадке?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 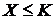 при следующих условиях. Одновременно бросаются 4 монеты. Х – число выпавших " орлов",
при следующих условиях. Одновременно бросаются 4 монеты. Х – число выпавших " орлов", 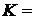 3.
3.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|