
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Индивидуальные задания к контрольной работе №11 1 страница
Индивидуальные задания к контрольной работе №11
Варианты расчетного задания по теме
" Теория вероятностей и математическая статистика"
Вариант № 1
1. Шесть ящиков различных материалов доставляются на 5 этажей стройки. Сколькими способами можно распределить ящики по этажам?
2. На пяти карточках написаны числа 1, 2, 3, 4, 5. Наудачу берут две карточки. Найти вероятность, что большее из извлеченных чисел равно 4.
3. Три стрелка выстрелили по мишени. При одном выстреле вероятность попадания для них равна 0, 5; 0, 7; и 0, 9 соответственно. Найти вероятность, что мишень поражена не менее двух раз.
4. В семи урнах содержится по 2 белых и 2 черных шара, а в трех урнах по 7 белых и 3 черных шара. Какова вероятность, что из урны, взятой наудачу, будет извлечен белый шар? Найти вероятность, что шар извлечен из урны с 7 белыми и 3 черными шарами, если он оказался белым.
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 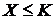 при следующих условиях. Ведется стрельба до первого попадания, но не свыше 5 выстрелов. Вероятность попадания при каждом выстреле равна 0, 7.
при следующих условиях. Ведется стрельба до первого попадания, но не свыше 5 выстрелов. Вероятность попадания при каждом выстреле равна 0, 7.  – число произведенных выстрелов,
– число произведенных выстрелов, 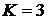 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 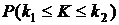 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 2; b) n=100, p=0, 002; c) n=100, p=0, 2, 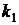 =16,
=16, 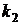 =40.
=40.
7. Плотность распределения 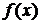 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 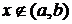
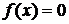 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 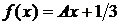 ,
,  =(0; 1),
=(0; 1),  =0, 5.
=0, 5.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 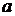 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 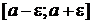 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 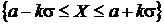 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 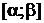 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 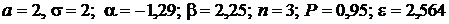 .
.
Вариант № 2
1. Сколькими способами можно расставить на шахматной доске 1 белый и 2 черных коня? Одноцветные фигуры неразличимы, кони могут стоять на любых клетках.
2. В лифт шестиэтажного дома на первом этаже вошло 4 человека. Каждый из них с одинаковой вероятностью выходит на любом из этажей, начиная со второго. Какова вероятность, что трое выйдут на одном этаже?
3. Для контроля за работой линии установлены три независимо работающих устройства, которые срабатывают при аварии с вероятностью 0, 8; 0, 9 и 0, 95 соответственно. Найти вероятность, что при аварии сработают два устройства.
4. Станок 30% времени обрабатывает деталь А и 70% – деталь В. При обработке детали А он простаивает 10% времени, а детали В – 15%. Какова вероятность застать станок простаивающим? Найти вероятность, что станок, который застали простаивающим, находится в режиме обработки детали В.
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 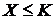 при следующих условиях. Партия из 20 деталей содержит 4 бракованных. Произвольным образом выбрали 5 деталей. X – число доброкачественных деталей среди отобранных, K=2.
при следующих условиях. Партия из 20 деталей содержит 4 бракованных. Произвольным образом выбрали 5 деталей. X – число доброкачественных деталей среди отобранных, K=2.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 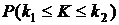 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 4; b) n=50, p=0, 004; c) n=150, p=0, 4, 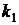 =12,
=12, 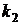 =56.
=56.
7. Плотность распределения 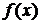 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 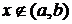
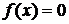 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 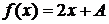 ,
,  =(0; 1),
=(0; 1),  =
= 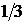 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 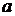 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 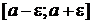 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 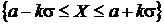 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 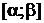 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 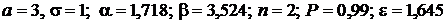 .
.
Вариант № 3
1. 15 занумерованных биллиардных шаров раскладывают по 6 лузам. Сколькими способами это можно сделать?
2. В коробке 10 красных, 6 зеленых и 8 синих карандашей. Три из них вынимают наугад. Найти вероятность того, что все карандаши разных цветов.
3. Из трех орудий производят залп по цели. Вероятность попадания при одном выстреле для первого орудия равна 0, 9, а для второго и третьего соответственно 0, 8 и 0, 6. Найти вероятность того, что только одно орудие попадает в цель.
4. Сборщик получает 45% деталей завода №1, 30% – завода №2, остальные – с завода №3. Вероятность того, что деталь первого завода отличного качества 0, 7; для деталей второго и третьего заводов эти вероятности соответственно равны 0, 8 и 0, 9. Найти вероятность, что наудачу взятая сборщиком деталь окажется отличного качества. Какова вероятность, что взятая наудачу деталь, оказавшаяся отличного качества, изготовлена заводом №1?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 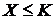 при следующих условиях. У стрелка, вероятность попадания которого в мишень равна 0, 65 при каждом выстреле, имеется 5 патронов. Стрельба прекращается при первом же попадании. Х – число оставшихся патронов,
при следующих условиях. У стрелка, вероятность попадания которого в мишень равна 0, 65 при каждом выстреле, имеется 5 патронов. Стрельба прекращается при первом же попадании. Х – число оставшихся патронов, 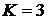 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 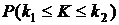 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 9; b) n=50, p=0, 002; c) n=192, p=0, 25, 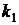 =40,
=40, 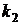 =56.
=56.
7. Плотность распределения 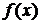 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 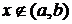
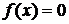 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 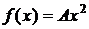 ,
,  =(0; 1),
=(0; 1),  =
= 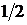 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 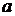 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 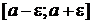 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 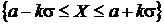 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 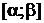 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 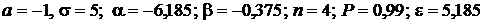 .
.
Вариант №4.
1. Из урны, содержащей 8 шаров с номерами 1, 2, …, 8, шары извлекают один за другим без возвращения и записывают их номера. Сколько различных записей можно получить?
2. Наудачу выбирается шестизначное число. Какова вероятность того, что число одинаково читается как слева направо, так и справа налево (например, 123321)?
3. В урне 2 белых, 3 черных и 5 красных шаров. Наугад извлекают три шара. Найти вероятность того, что они одного цвета.
4. Деталь проходит одну из трех операций обработки с вероятностью 0, 25; 0, 35; 0, 40 соответственно. Вероятность получения брака на первой операции равна 0, 02, на второй – 0, 04, а на третьей – 0, 05. Найти вероятность получения брака после обработки. Какова вероятность, что деталь прошла третью операцию обработки, если получен брак?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 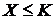 при следующих условиях. Прибор содержит три элемента, вероятности отказов которых за определенное время независимы и равны соответственно 0, 15; 0, 20 и 0, 25. Х – число отказавших элементов,
при следующих условиях. Прибор содержит три элемента, вероятности отказов которых за определенное время независимы и равны соответственно 0, 15; 0, 20 и 0, 25. Х – число отказавших элементов, 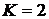 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 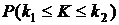 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=5, p=0, 5; b) n=20, p=0, 01; c) n=100, p=0, 1, 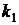 =5,
=5, 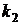 =15.
=15.
7. Плотность распределения 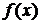 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 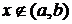
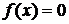 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 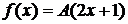 ,
,  =(0; 2),
=(0; 2),  =
= 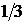 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 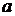 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 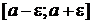 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 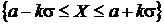 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 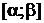 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 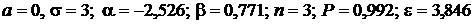 .
.
Вариант №5.
1. Сколькими способами из 25 студентов группы можно: a) выбрать актив в составе: староста, культорг, профорг; b) выбрать трех дежурных?
2. Бросаются одновременно три игральные кости. Найти вероятность того, что сумма выпавших очков кратна 5.
3. Электрическая цепь составлена по схеме (рис. 1). Элементы цепи
выходят из строя независимо друг от друга с вероятностью 0, 2; 0, 1; 0, 3 соответственно. Найти вероятность того, что цепь будет пропускать ток.
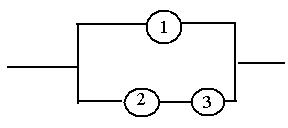
Рис. 1
4. По цели производятся три выстрела с вероятностью попадания 0, 2 при каждом. Вероятность уничтожения цели при одном попадании равна 0, 3; при двух попаданиях – 0, 6; при трех – 0, 9. Найти вероятность уничтожения цели. Какова вероятность, что было одно попадание, если цель уничтожена?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 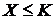 при следующих условиях. В урне 4 белых и 3 черных шара. Наудачу один за другим извлекаем шары из урны до появления белого шара. Х – число извлеченных черных шаров,
при следующих условиях. В урне 4 белых и 3 черных шара. Наудачу один за другим извлекаем шары из урны до появления белого шара. Х – число извлеченных черных шаров,  .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 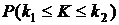 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
Дано: a) n=4, p=0, 15; b) n=20, p=0, 015; c) n=400, p=0, 2, 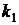 =75,
=75, 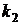 =100.
=100.
7. Плотность распределения 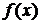 случайной величины
случайной величины  на
на  задана в условии задачи, а при
задана в условии задачи, а при 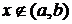
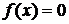 . Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение
. Требуется: 1) найти параметр A; 2) построить графики плотности и функции распределения; 3) найти математическое ожидание M[X], дисперсию D[X] и среднее квадратическое отклонение  ; 4) вычислить вероятность
; 4) вычислить вероятность  того, что отклонение случайной величины от математического ожидания не более заданного числа
того, что отклонение случайной величины от математического ожидания не более заданного числа  .
.
Дано: 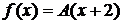 ,
,  =(0; 2),
=(0; 2),  =
= 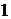 .
.
8. Случайное отклонение размера детали от номинала распределено по нормальному закону с математическим ожиданием 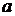 и средним квадратическим отклонением
и средним квадратическим отклонением  . Годными считаются детали, для которых отклонение от номинала лежит в интервале
. Годными считаются детали, для которых отклонение от номинала лежит в интервале 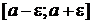 . Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал
. Требуется: 1) записать формулу плотности распределения и построить график плотности; 2) найти вероятность попадания случайной величины в интервал 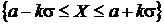 ; 3) найти вероятность попадания n случайно выбранных деталей в интервал
; 3) найти вероятность попадания n случайно выбранных деталей в интервал 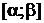 ; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем
; 4) определить, какое наименьшее число деталей необходимо изготовить, чтобы среди них с вероятностью не меньшей, чем  , хотя бы одна деталь была годной.
, хотя бы одна деталь была годной.
Замечание. В пп. 3, 4 пользоваться линейной интерполяцией при отсутствии нужного значения в таблице.
Дано: 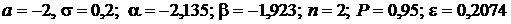 .
.
Вариант №6.
1. Из цифр 1, 2, 3, 4, 5, 6, 7, 8, 9 составляются всевозможные пятизначные числа, не содержащие одинаковых цифр. Каково максимальное число таких чисел?
2. Из полного комплекта домино извлекается наудачу одна кость. Чему равна вероятность того, что сумма очков на обеих половинках этой кости окажется равной 7?
3. Электрическая цепь составлена по схеме (рис. 2). Элементы цепи
выходят из строя с вероятностью 0, 1; 0, 4; 0, 5; 0, 2 соответственно. Найти вероятность, что цепь будет пропускать ток.
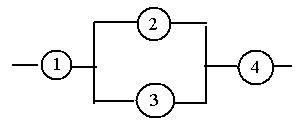
Рис. 2
4. В первой урне 4 белых и 6 черных шаров, во второй 5 белых и 4 черных. Из первой урны во вторую перекладывают, не глядя, один шар, после чего из второй урны извлекают один шар. Найти вероятность, что этот шар белый. Какова вероятность, что из первой во вторую урну был переложен черный шар, если извлеченный из второй урны шар оказался белым?
5. Найти закон распределения, математическое ожидание и дисперсию случайной величины  . Построить график функции распределения и найти вероятность события
. Построить график функции распределения и найти вероятность события 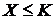 при следующих условиях. На пути автомашины 4 независимых друг от друга светофора, каждый из которых с вероятностью 0, 4 запрещает движение. Х – число пройденных до первой остановки светофоров,
при следующих условиях. На пути автомашины 4 независимых друг от друга светофора, каждый из которых с вероятностью 0, 4 запрещает движение. Х – число пройденных до первой остановки светофоров, 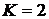 .
.
6. В случаях a, b, c рассматривается серия из n независимых опытов с двумя исходами в каждом – " успех" или " неуспех". Вероятность " успеха" равна p, " неуспеха" q=1-p в каждом испытании. X – число " успехов" в n испытаниях. Требуется:
1) для случая a (малого n) построить ряд распределения, функцию распределения X, найти M[X], D[X] и  ;
;
2) Для случая b (большого n и малого p) найти  приближенно с помощью распределения Пуассона. Оценить точность приближения;
приближенно с помощью распределения Пуассона. Оценить точность приближения;
3) для случая с (большого n) найти вероятность 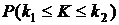 приближенно с помощью теоремы Муавра-Лапласа.
приближенно с помощью теоремы Муавра-Лапласа.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|