Прямая пропорциональность.. 3. Кубическая.. 5. Модуль х.. 10. Арккосинус.. 11. Тангенс.

Прямая пропорциональность.

Уравнение 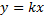График – прямая, проходящая через начало координат

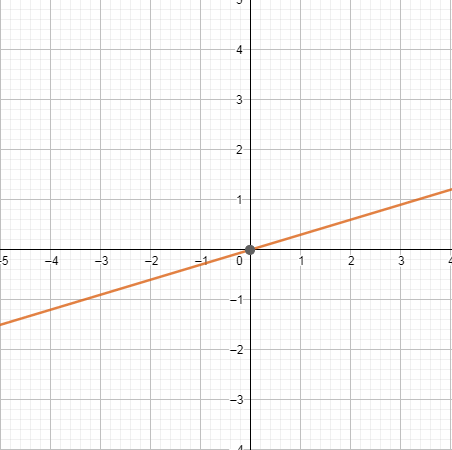
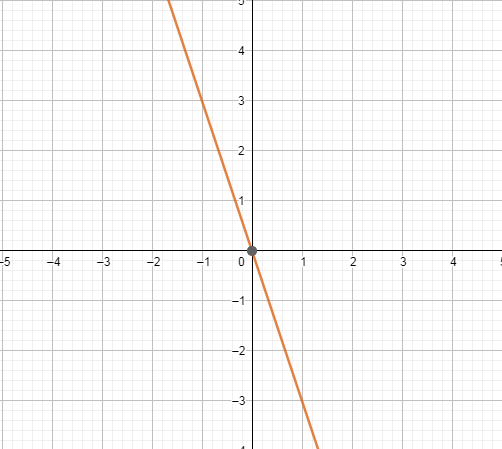
При k> 0 - возрастает при k< 0 - убывает

2. 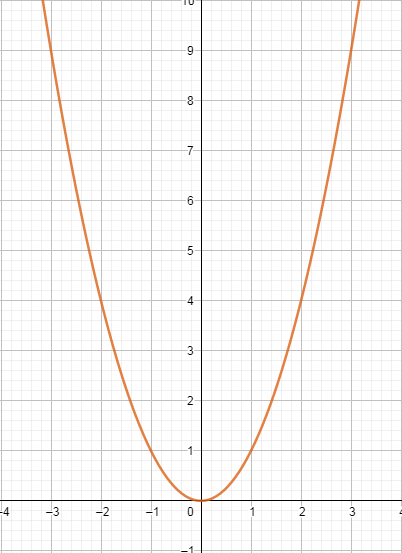Квадратичная.

Уравнение

График – парабола, ветви которой направлены вверх

и вершина находится в начале координат (0; 0)

D(y)=(-∞; +∞ )

Е(y)=[0; +∞ )

Уравнение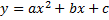

График – парабола c вершиной в точке (x₀; y₀ ), где ;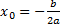

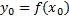
D(y)=(-∞; +∞ )                                 D(y)=(-∞; +∞ )

Е(y)=[ 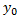; +∞ )                                 Е(y)=(-∞; ]



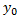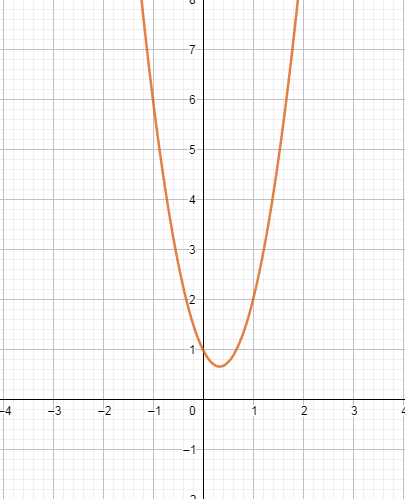
                                    При a> 0 – ветви вверх                           при a< 0 – ветви вниз

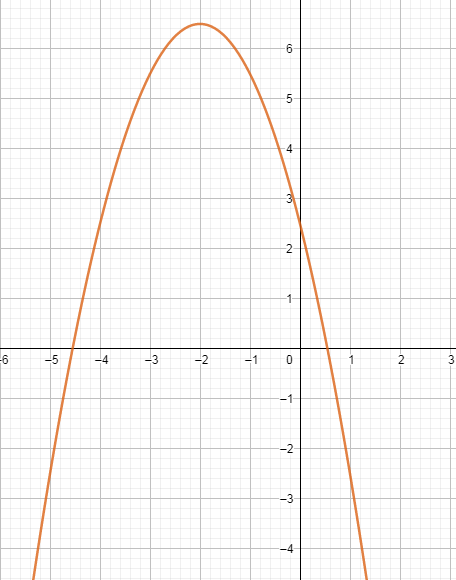
3. Кубическая.

Уравнение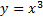

         График – кубическая парабола

D(y)=(-∞; +∞ )

Е(y)= (-∞; +∞ )

4. 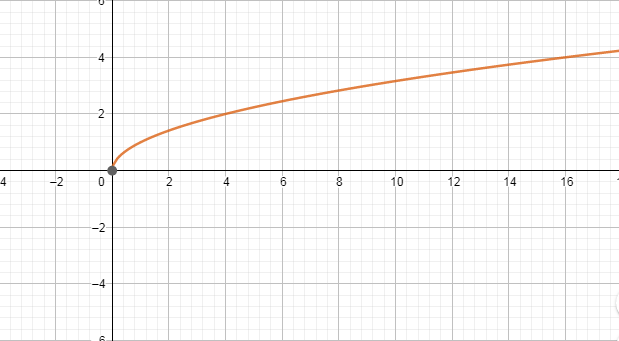Корень из х.

Уравнение

D(y)=[0; +∞ )

Е(y)=[0; +∞ )

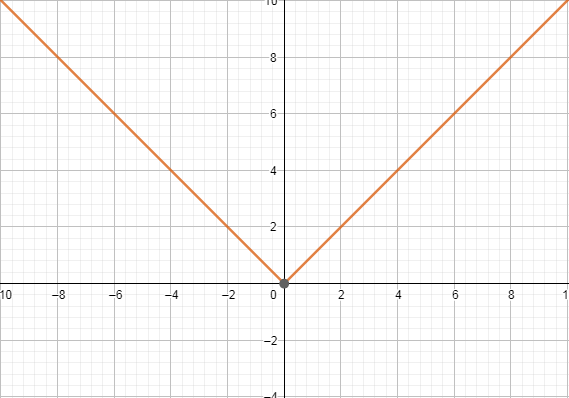
5. Модуль х.

Уравнение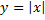

D(y)=(-∞; +∞ )

Е(y)=[0; +∞ )

6. Обратная пропорциональность.

Уравнение 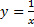                       График – гипербола

D(y)=(-∞; 0)U(0; +∞ )                                    Е(y)=(-∞; 0)U(0; +∞ )



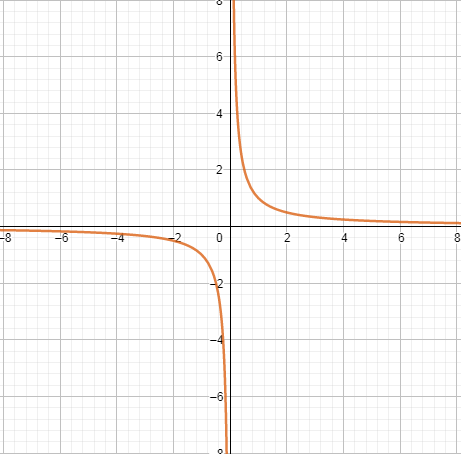
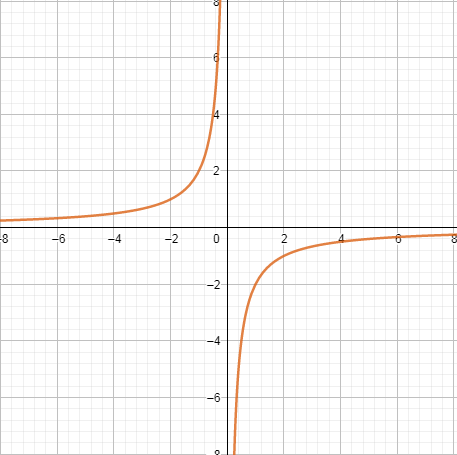
                    При k> 0 - в 1 и 3 четвертях                    при k< 0 - во 2 и 4 четвертях

7. 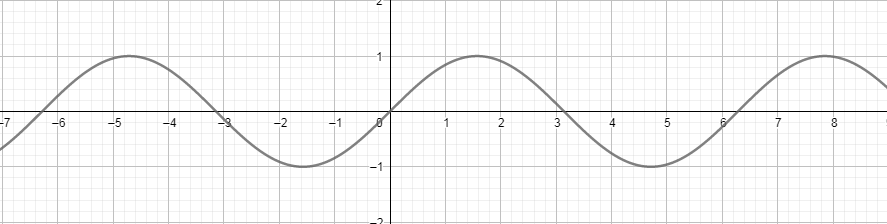Синус.

Уравнение

График – синусоида.

D(y)=(-∞; +∞ )

Е(y)=[-1; 1]

8. 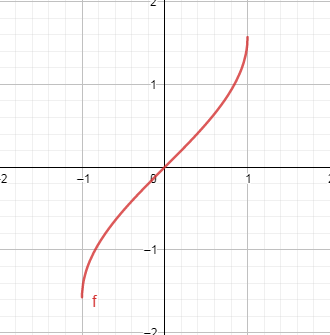Арксинус.

Уравнение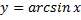

D(y)=[-1; 1]

Е(y)=[- ; ]

9. Косинус.

Уравнение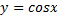

        График – синусоида.

D(y)=(-∞; +∞ )   Е(y)=[-1; 1]

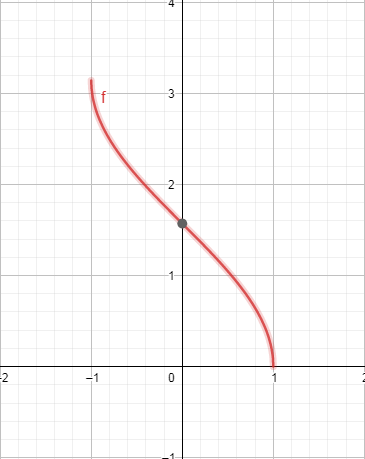
10. Арккосинус.

Уравнение 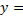arccosx

D(y)=[-1; 1]

Е(y)=[0; π ]

11. Тангенс.

Уравнение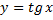

График – тангенсоида.

D(y)=(x≠ ; nϵ Z)

Е(y)= (-∞; +∞ )

12. 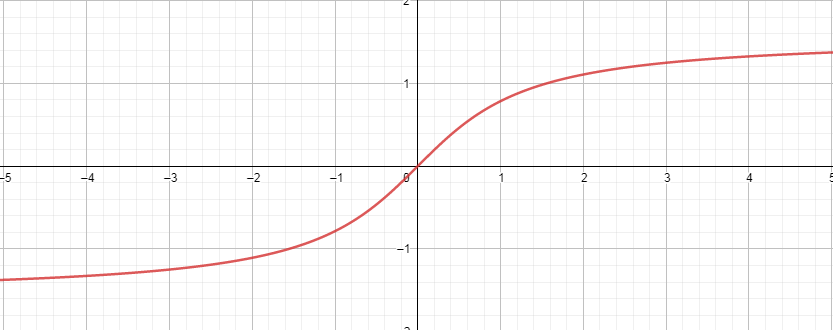Арктангенс.

Уравнение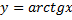

D(y)= (-∞; +∞ )

Е(y)=(- ; )

13. Котангенс.

Уравнение

График – тангенсоида

D(y)=(x≠ ; nϵ Z)

          Е(y)= (-∞; +∞ )

14. Арккотангенс.

Уравнение

D(y)= (-∞; +∞ )

Е(y)=(0; π )

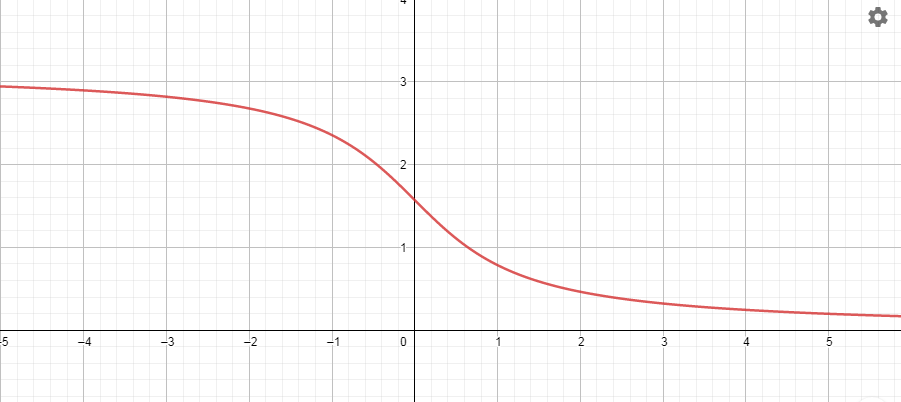
15. Показательная.

Уравнение 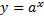  График – экспонента.      Пересекает ось Y в точке (0; 1)

D(y)=(-∞; +∞ )                                 D(y)=(-∞; +∞ )

Е(y)=( 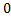; +∞ )                                 Е(y)= )=( ; +∞ )



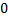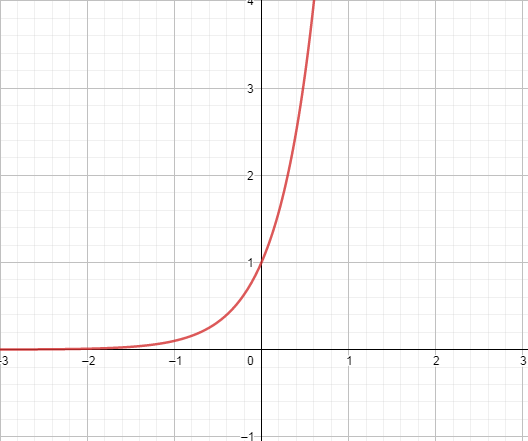
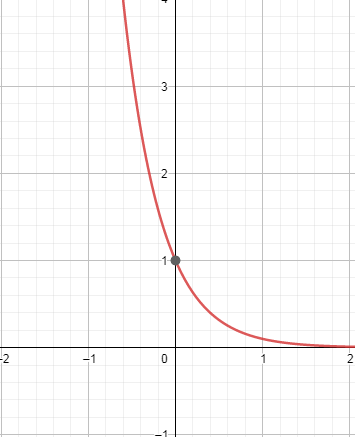
                             При a> 1 – возрастает                        при 0< a< 1 – убывает

16. Логарифмическая.

Уравнение 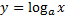График – экспонента. Пересекает ось Y в точке (1; 0)

D(y)=( 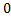; +∞ )                                 D(y)=(0; +∞ )

Е(y)=(-∞; +∞ )                         Е(y)= (-∞; +∞ )



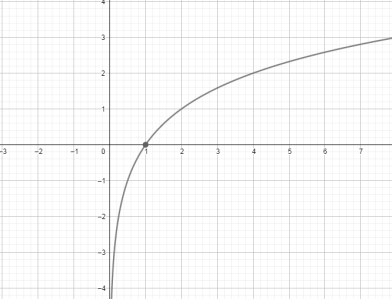
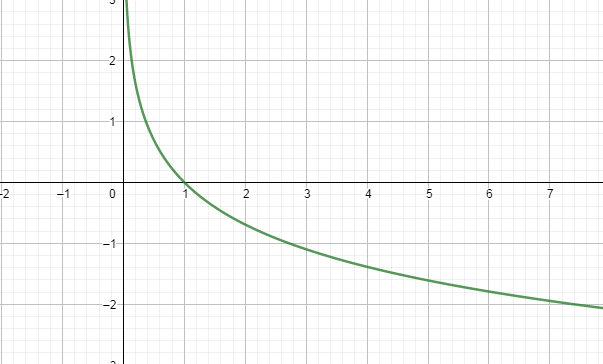
               При a> 1 – возрастает                       при 0< a< 1 – убывает

⇐ Предыдущая 1 234 Следующая ⇒