2. Непрерывность.

Функция –

это зависимость одной переменной (y - значение функции) от другой ( х - аргумент), при которой каждому значению аргумента соответствует единственное значение функции.

Свойства функции:

1. Область определения D(y) –это все допустимые значения х

1. Если в функции содержится выражение, содержащее х в знаменателе

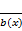, то решаем уравнение 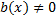и его корни исключаем из числовой прямой

2. Если в функции содержится выражение содержащее х под знаком корня чётной степени

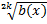, то решаем неравенство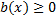

3. Если в функции содержится выражение, содержащее х под знаком логарифма или в основании логарифма

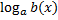, то решаем неравенство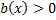

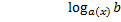, то решаем неравенство ,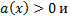

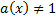4. Если в функции содержится выражение, содержащее х под знаком тангенса

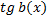, то решаем уравнение 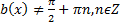и его корни исключаем из числовой прямой

5. Если в функции содержится выражение, содержащее х под знаком котангенса

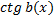, то решаем уравнение 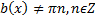и его корни исключаем из числовой прямой,

оставшиеся промежутки записываем в область определения

Те же действия производятся и при решении уравнений и неравенств, чтобы найти Область Допустимых Значений. Корни уравнения могут принадлежать только ОДЗ!

2. Непрерывность.

Если какие-то точки пришлось «выколоть» при нахождении области определения, то функция будет терпеть разрыв, то есть график нельзя нарисовать одной линией. Если областью определения является (-∞; +∞ ), то есть любое действительное число, то функция будет непрерывна.

12 3 4 Следующая ⇒