
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчет сечения колонны по I варианту армирования 3 страница
7. По величине пролетного и опорных моментов в каждом пролете ригеля определяется приложенная к ним приведенная погонная нагрузка:
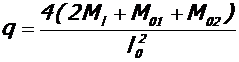 ,
,
Ml - величина момента в середине пролета, М01 и М02 - величина опорных моментов у граней колонн, l0 =6, 2-0, 4=5, 8 м - длина рассматриваемого пролета ригеля в свету.
7. 1. Для крайнего пролета крайнего ригеля.
а) полная нагрузка
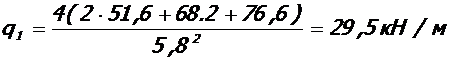
б)полная пониженная нагрузка
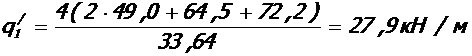
в) постоянная нагрузка
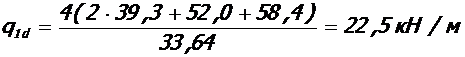
7. 2. Результаты расчета приведенной погонной нагрузки на ригели сведены в таблицу 5.
Таблица 5.
| Пролет | Ригель | Нагрузка, вид | Значение погонной нагрузки q, кН/м |
|
Крайний |
крайний | полная | 29, 5 |
| полная пониженная | 27, 9 | ||
| постоянная | 22, 5 | ||
|
средний | полная | 45, 6 | |
| полная пониженная | 41, 8 | ||
| постоянная | 34, 7 | ||
|
Средний | крайний | полная | 29, 7 |
| постоянная | 22, 4 | ||
| средний | полная | 45, 4 | |
| постоянная | 34, 5 |
8. Длина участков пролетов ригелей с трещинами:
- в середине пролета lcrcl = l0 – 2x1;
где: l0 - длина пролета ригеля в свету между гранями колонн,
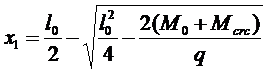 , q и М - см. п. 7, выше.
, q и М - см. п. 7, выше.
- у колонн 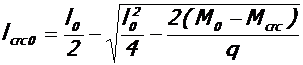
8. 1. Длина участков с трещинами крайнего ригеля в крайнем пролете.
а) при полной нагрузке.
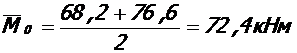 , Мcrc = 11, 2 кНм,
, Мcrc = 11, 2 кНм,
q1 = 29, 5 кН/м,
l0 = 6, 2-0, 4 = 5, 8 м.
- в пролете
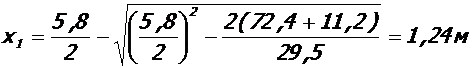 ,
,
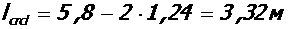 ;
;
- у колонн
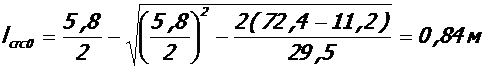 ;
;
б) при полной пониженной нагрузке:
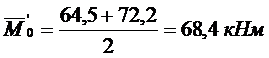 ; q' = 27, 0 кН/м;
; q' = 27, 0 кН/м;
- в пролете:
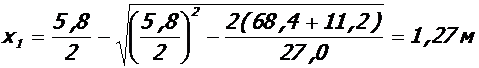 ,
,
lcrcl = 5, 8-2·1, 27 = 3, 26 м;
- у колонн
 ;
;
в) при постоянной нагрузке:
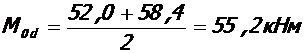 ; qd = 22, 5 кН/м.
; qd = 22, 5 кН/м.
- в пролете:
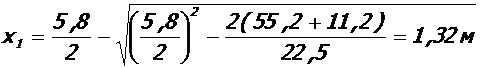 ;
;
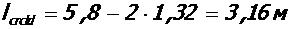 ;
;
- у колонн:
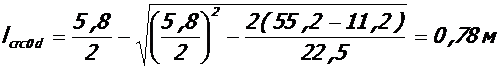 .
.
7. 2. Результаты расчета длин участков ригелей с трещинами, определенные аналогично п. 7. 1 сведены в таблицу 6.
Таблица 6.
| Пролет | Ригель | Нагрузка | Среднее значение опорного момента | Длина участков с трещинами, м | |
| в пролете lcrcl, м | у колонн lcrc0, м | ||||
| Крайний | крайний | полная | 72, 4 | 3, 32 | 0, 84 |
| полная пониж. | 68, 4 | 3, 26 | 0, 82 | ||
| постоянная | 55, 2 | 3, 16 | 0, 78 | ||
| средний | полная | 112, 7 | 3, 38 | 0, 88 | |
| полная пониж. | 103, 3 | 3, 34 | 0, 87 | ||
| постоянная | 85, 8 | 3, 26 | 0, 83 | ||
| Средний | крайний | полная | 76, 6 | 3, 16 | 0, 90 |
| постоянная | 58, 4 | 2, 96 | 0, 85 | ||
| средний | полная | 117, 1 | 3, 24 | 0, 93 | |
| постоянная | 89, 2 | 3, 12 | 0, 89 | ||
9. Абсолютное удлинение продольной оси каждого пролета li несущих ригелей, вызванное образованием поперечных вертикальных трещин, определяется из выражения:
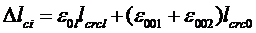 ,
,
где значения ε 0l и ε 00, lcrcl и lcrc0 см. табл. 4 и 6.
9. 1. Абсолютное удлинение оси крайнего пролета крайнего ригеля.
а) от полной нагрузки:
ε 0l = 1, 43·10-3; ε 001 = 1, 75·10-3; ε 002 = 1, 72·10-3 (табл. 4)
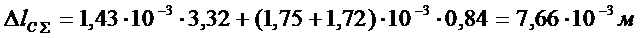 ;
;
б) от полной пониженной нагрузки:
ε 0l = 1, 25·10-3; ε 001 = 1, 39·10-3; ε 002 = 1, 49·10-3 (табл. 4)
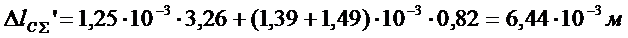 ;
;
в) от постоянной нагрузки:
ε 0l = 8, 13·10-4; ε 001 = 1, 15·10-3; ε 002 = 9, 61·10-4 (табл. 4)
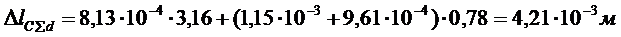 .
.
9. 2. Результаты расчета абсолютного удлинения продольной оси каждого пролета ригелей, вызванного образованием поперечных трещин, сведены в таблицу 7.
Таблица 7
| Пролет | Ригель | Нагрузка | Абсолютное удлинение продольной оси ригеля, Δ l, м |
| Крайний | крайний | полная | 7, 66·10-3 |
| полная пониж. | 6, 44·10-3 | ||
| постоянная | 4, 21·10-3 | ||
| средний | полная | 7, 92·10-3 | |
| полная пониж. | 6, 20·10-3 | ||
| постоянная | 4, 40·10-3 | ||
| Средний | крайний | полная | 7, 52·10-3 |
| постоянная | 3, 89·10-3 | ||
| средний | полная | 6, 97·10-3 | |
| постоянная | 3, 95·10-3 |
10. Величина продольного распора в несущих ригелях.
10. 1. В крайних пролетах величину распора Hr рассчитывают по величине удлинения продольной оси ригеля, создаваемого приращением временной нагрузки в пределах от пониженной полной до полной, по жесткостному отпору колонн и бортовых связевых ригелей наружного контура каркаса. Расчет с учетом указанных факторов выполняется по формуле:
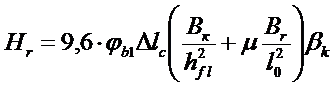 ,
,
где: φ b1 = 0, 85 - коэффициент, учитывающий кратковременную ползучесть бетона при изменениях временной нагрузки; ∆ lc - приращение удлинения несущих ригелей в крайних пролетах от перепада нагрузки (табл. 7); Вk - жесткость поперечного сечения колонны при изгибе; Вr - то же, связевого ригеля при изгибе в горизонтальной плоскости; hfl и l0 - высота этажа и длина в свету пролета примыкающих связевых ригелей, соответственно; β k - коэффициент, учитывающий условия примыкания к бортовому ригелю, β k=0, 9, m=0, 65 - при примыкании рассчитываемого несущего ригеля к угловой колонне и β k=1, 2, m=1, 0 - при примыкании несущего ригеля к колоннам бокового ряда.
Для настоящего примера:
Вк = ЕbIк = 30·106·0, 44/12 = 64000 кНм2,
Вr = 30·106·0, 26·0, 53/12= 81250 кНм2, hfl = 3, 0 м; l0 = 5, 8 м.
Для крайнего ригеля величина Hr составляет при
∆ lc = 7, 66·10-3 - 6, 44·10-3 = 1, 22·10-3 м (см. табл. 7)

Для среднего ригеля величина Hr составляет при
∆ lc = 7, 92·10-3 - 6, 20·10-3 = 1, 72·10-3 м (см. табл. 7)
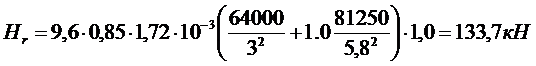
10. 2. В средних пролетах ригелей величину реактивного продольного распора определяют по величине удлинения их продольной оси от полной нагрузки за вычетом удлинения, вызванного постоянной и длительной нагрузкой и рассчитывают по формуле:
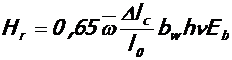 ,
,
но не более
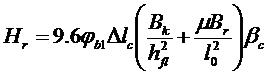 (*)
(*)
здесь: 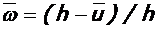 - коэффициент, учитывающий влияние высоты u трещин на жесткость сечения ригеля,
- коэффициент, учитывающий влияние высоты u трещин на жесткость сечения ригеля, 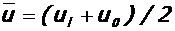 - средняя наибольшая высота трещин в пролете (ul) и у колонн (u0); b и h - ширина и высота сечения ригеля, в котором определяется продольный распор, bс=2, 05 и m=0, 65 – для крайнего несущего ригеля, bс=2, 25 и m=1, 0 – для среднего несущего ригеля, остальные обозначения приведены выше.
- средняя наибольшая высота трещин в пролете (ul) и у колонн (u0); b и h - ширина и высота сечения ригеля, в котором определяется продольный распор, bс=2, 05 и m=0, 65 – для крайнего несущего ригеля, bс=2, 25 и m=1, 0 – для среднего несущего ригеля, остальные обозначения приведены выше.
Для крайнего ригеля: b = 0, 5 м, h = 0, 26 м, l0 = 5, 8 м
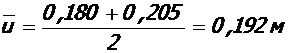 (см. табл. 3);
(см. табл. 3); 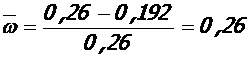 ;
;
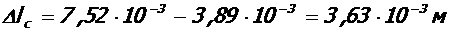 (см. табл. 7)
(см. табл. 7)
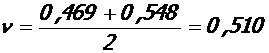 (см. табл. 4)
(см. табл. 4)
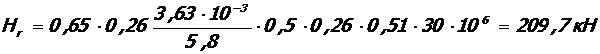
Проверка условия (*): при
Br = Eb h bw3 / 12 = 30·106·0. 26·0. 53 / 12 = 81250 кНм2;
Принято: Hr = 209, 7 < 527, 1 кН.
Для среднего ригеля: b = 0, 6 м
 ;
; 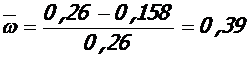 ;
;
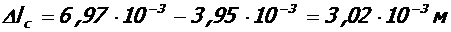 ;
; 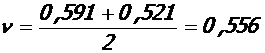 ;
;
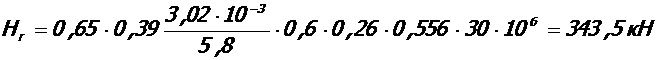
Проверка условия (*):
Принято: Hr = 343, 5 < 528, 2 кН.
11. Величина моментов, разгружающих расчетные сечения несущих ригелей при действии продольного распора, определяют по формуле:
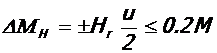 ,
,
где M – значение изгибающего момента от полной расчетной нагрузки, определенное в рассматриваемом сечении по упругому расчету каркаса; u - высота трещины в расчетном сечении ригеля от полной расчетной нагрузки (см. табл. 3).
11. 1. В крайнем пролете крайнего ригеля Hr = 77, 8 кН
- в середине пролета u = 0, 201 м; М=51, 6 кНм
\∆ М\=77, 8·0, 201/2=7, 8 кНм < 0. 2∙ 51, 6=10, 3 кНм
- у крайней (угловой) колонны u = 0, 191 м; М=68, 2 кНм
\∆ М\=77, 8∙ 0, 191/2=7, 4 кНм < 0. 2∙ 68, 2=13, 6 кНм
- у средней колонны u = 0, 180 м; М=76, 6 кНм
\∆ М\=77, 8∙ 0, 180/2=7, 0 кНм < 0. 2∙ 76, 6=15, 3 кНм
11. 2. В среднем пролете крайнего ригеля Hr = 209, 7 кН
- в середине пролета u = 0, 205 м; М = 48, 4 кНм;
\∆ М\=209, 7∙ 0, 205/2=21, 5 кНм > 0. 2∙ 48. 4=9, 7 кНм
- у колонн u = 0, 180 м; М = 76. 6 кНм;
\∆ М\=209, 7∙ 0, 180/2=18, 9 кНм > 0. 2∙ 76. 6=15, 3 кНм
11. 3. В крайнем пролете среднего ригеля Hr = 160, 4 кН
- в середине пролета u = 0, 194 м; М = 79, 2 кНм;
\∆ М\=133. 7∙ 0, 194/2=13, 0 кНм < 0. 2∙ 79. 2=15, 8 кНм
- у крайней колонны u = 0, 157 м; М = 108, 3 кНм;
\∆ М\=133. 7∙ 0, 157/2=10, 5 кНм < 0. 2∙ 108. 3=21, 7 кНм;
- у средней колонны u = 0, 127 м; М = 117, 1 кНм.
\∆ М\=133. 7∙ 0, 127/2=8, 5 кНм < 0. 2∙ 117. 1=23, 4 кНм;
11. 4. В среднем пролете среднего ригеля Hr = 343, 5 кН
- в середине пролета u = 0, 190 м; М = 73, 8 кНм;
\∆ М\=343, 5∙ 0, 190/2=32, 6 кНм > 0. 2∙ 73. 8=14, 8 кНм;
- у колонн u = 0, 127 м; М = 117, 1 кНм.
\∆ М\=343, 5∙ 0, 127/2=21, 8 кНм < 0. 2∙ 117. 1=23, 4 кНм;
12. Абсолютные значения величины моментов Мн в расчетных сечениях ригелей от действия полной расчетной нагрузки с учетом распора Нr определяем по меньшему значению ∆ М, определенному выше в п. 11.
|Мн| = |М| - |∆ Мн|,
где |М| - значение по модулю величины момента, определенной по упругому расчету каркаса.
Таким образом, значение величины момента М для окончательного определения требуемой площади сечения рабочей арматуры в расчетных сечениях расчетных ригелей могут быть установлены.
12. 1. В крайнем пролете крайнего ригеля:
- в середине пролета Мн = 51, 6-7, 8=43, 8 кНм;
- у средней колонны Мн = 76, 6-7, 4=69, 2 кНм;
- у крайней (угловой) колонны Мн = 68, 2-7, 0=61, 2 кНм.
12. 2. В среднем пролете крайнего ригеля:
- в середине пролета Мн = 48, 4-9, 7=38, 7 кНм;
- у колонн Мн = 76, 6-15, 3=61, 3 кНм;
12. 3. В крайнем пролете среднего ригеля:
- в середине пролета Мн = 79, 2-13, 0=66, 2 кНм;
- у средней колонны Мн = 117, 1-8, 5=108, 6 кНм.
- у угловой колонны Мн = 108, 3-10, 5=97, 8 кНм;
12. 4. В среднем пролете среднего ригеля:
- в середине пролета Мн = 73, 8-14, 8=59, 0 кНм;
- у колонн Мн = 117, 1-21, 8=96, 0 кНм.
12. 5. С учетом установленных значений Мн произведен перерасчет требуемого сечения рабочей арматуры в ригелях. Результаты расчета представлены в табл. 8. Согласно исходным условиям примера: рабочее армирование - сталь класса А500с, бетон класса B25.
Таблица 8
| Пролет | Ригель | Сечение | Начальные значения | Окончательное значение | |||||
| |М|, кНм | Рабочее армирование | |Мн|, кНм | Рабочее армирование | Сокращение площади сечения рабочей арматуры, % | |||||
| Вид | Площадь, м2 | Вид | Площадь, м2 | ||||||
| Крайний | Крайний | середина пролета | 51, 6 | 5ø 12 Ат500С | 5, 65·10-4 | 43, 8 | 4ø 12 А500с | 4, 52·10-4 | 20, 0 |
| у крайней колонны | 68, 2 | 2ø 20 + 1ø 12 | 7, 41·10-4 | 61, 2 | 2ø 20 + 1ø 8 | 6, 78·10-4 | 8, 5 | ||
| у средней колонны | 76, 6 | 2 ø 20 + 2ø 12 | 8, 54·10-4 | 69, 2 | 2ø 20 + 1ø 12 | 7, 41·10-4 | 13, 2 | ||
| Средний | середина пролета | 79, 2 | 2ø 20 + 2 ø 12 | 8, 54·10-4 | 66, 2 | 2ø 20 +1 ø 12 | 7, 41·10-4 | 13, 2 | |
| у крайней колонны | 108, 3 | 2 ø 25 + 3 ø 12 | 1, 32·10-3 | 97, 8 | 3ø 20 +1ø 12 | 1, 17·10-3 | 11, 4 | ||
| у средней колонны | 117, 1 | 3 ø 25 + 2 ø 12 | 1, 70·10-3 | 108, 6 | 4ø 20 | 1, 26·10-3 | 25, 9 | ||
| Средний | Крайний | середина пролета | 48, 4 | 5 ø 12 | 5, 65·10-4 | 38, 7 | 4ø 12 | 4, 52·10-4 | 20, 0 |
| у колонны | 76, 6 | 2 ø 20 + 2 ø 12 | 8, 54·10-4 | 61, 3 | 2ø 20 + 1ø 8 | 6, 78·10-4 | 20, 6 | ||
| Средний | середина пролета | 73, 8 | 2 ø 20 + 2 ø 12 | 8, 54·10-4 | 59, 0 | 2ø 20 | 6, 28·10-4 | 26, 5 | |
| у колонны | 117, 1 | 3 ø 25 + 2 ø 12 | 1, 70·10-3 | 96, 0 | 4ø 20 | 1, 26·10-3 | 25, 9 | ||
Вывод . С учетом влияния продольного реактивного распора Hr. окончательную площадь сечения рабочей арматуры несущих ригелей следует принять по данным табл. 8.
Пример 5
Проверить прочность сечений колонны рамно-связевого каркаса под высокие расчетные нагрузки. Колонна содержит продольную арматуру из высокопрочной стали класса Ат-1000 ГОСТ 10884-94 и косвенное армирование в виде сварных сеток из стали класса Ат-500С, установленных равномерно по высоте колонны (в соответствии со СНиП 2. 03. 01-84*). Колонна может быть выполнена из монолитного или сборного железобетона.
Расчет выполняется по методике СНиП 2. 03. 01-84*.
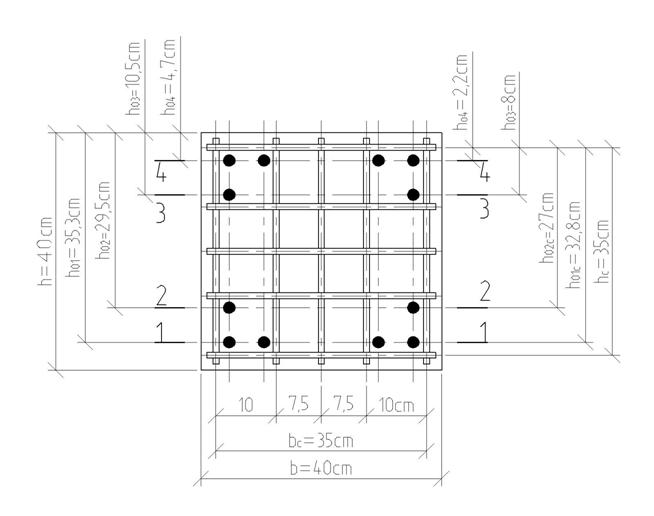
Рис. П. 4. Сечение колонны с косвенным армированием
Исходные данные: сечение колонны 40 х 40 см. Бетон класса В40 (Rb=22, 0 МПа, Rb, ser=29, 0 МПа, Eb=36 103 МПа). Продольная арматура – 12 стержней диаметром 25 мм класса Ат-1000. Площадь сечения одного стержня аs1=4, 91× 10-4м2 (Rs=815 МПа, Rs, ser=980 МПа, Rsc=400 МПа, Es=19× 104 МПа). Поперечная арматура – сварные сетки из стержней диаметром 10 мм класса А500с по пять стержней в каждом направлении. Площадь сечения одного стержня аs2=7, 85× 10-5м2. Расстояние между крайними стержнями сетки (по осям) – 35 см, шаг сеток по высоте колонны S=10 см. (Rs, xy = 450 МПа, Rs, ser = 500 МПа, Rsc = =400 МПа, Es=20× 104 МПа).
Полное продольное усилие от расчетного сочетания нагрузок по I группе предельных состояний NI = 6, 86 МН (700 т. с. ).
То же по II группе предельных состояний NII = 5, 68 МН (580 т. с. ).
Высота этажа 5, 0 м, расчетная длина колонны l0 = 3, 6 м.
Соотношение между усилиями Ml (от постоянной и длительной нагрузки) и М (от полной нагрузки) составляет 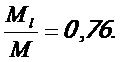
Расчет А. Прочность сечения колонны.
1. Расчетное значение случайного эксцентриситета продольного усилия N составляет
е0= b==1, 33× 10-2м.
Расчет ведется по недеформированной схеме с учетом влияния прогиба на прочность колонны.
2. Расчет прочности сечения колонны по I предельному состоянию заключается в проверке прочности ядра колонны в пределах части сечения, ограниченной площадью плана сварных сеток
hc=bc=0, 35м, h01c=0, 328м, h02c=0, 270м, h03c=8, 0× 10-2м,
h04c=ac=2, 2× 10-2 м, (см. рис. П. 4).
3. Геометрические характеристики.
- Радиус инерции ядра колонны:
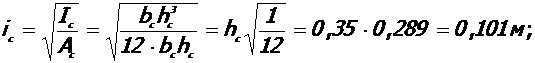
- Гибкость колонны (по ядру):
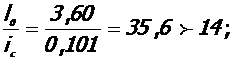
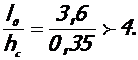
- Момент инерции сечения ядра колонны 
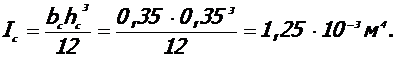
- Момент инерции сечения продольной арматуры:
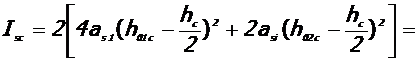
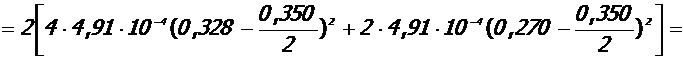
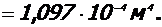
Момент инерции бетонной части сечения ядра:
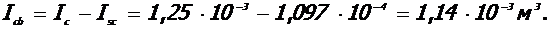
4. Расчет коэффициентов
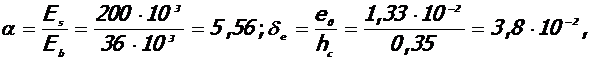
но не менее
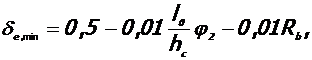 где Rb в МПа.
где Rb в МПа.
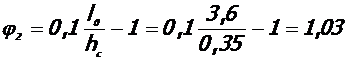 принимается
принимается 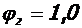
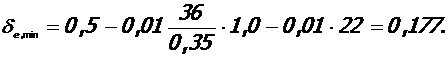
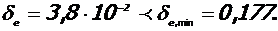
Для дальнейшего расчета принято 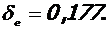
Коэффициент, учитывающий работу колонны частью сечения:
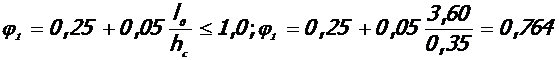 .
.
Коэффициент, учитывающий влияние длительного действия нагрузки на прогиб колонны в предельном состоянии:
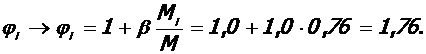
Условная критическая сила для ядра колонны:
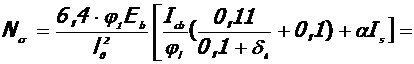
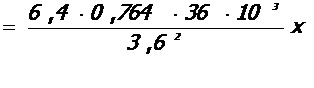
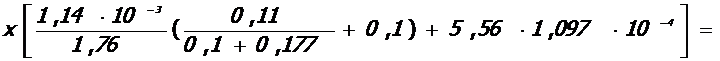 = 11, 907 МН.
= 11, 907 МН.
Коэффициент учета влияния прогиба на эксцентриситет продольного усилия: 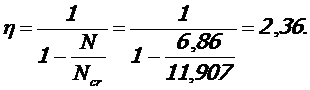
5. Эксцентриситет продольной силы N относительно центра тяжести арматуры, наиболее удаленной от точки приложения силы N:
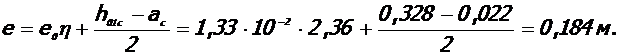
6. Момент продольной силы Nр =6, 86 МН относительно той же оси:
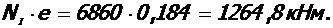
7. Расчетное сопротивление бетона сжатию в ядре колонны с учетом влияния косвенного армирования:
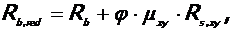
где: 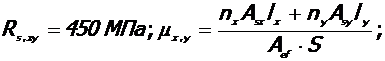 nx=ny=5
nx=ny=5
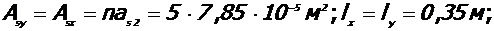
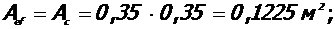
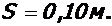
Коэффициент объемного армирования:
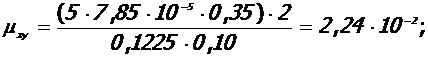
Коэффициент эффективности косвенного армирования
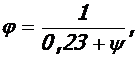
где 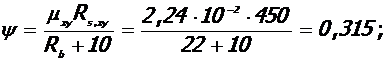

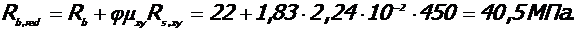
8. Расчетное сопротивление сжатию Rsc, red продольной высокопрочной арматуры:
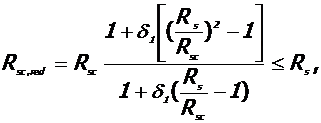
где: 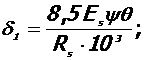 в котором
в котором 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|
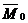 , кН/м
, кН/м