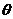- Р Р‡.МессенРТвЂВВВВжер
- ВКонтакте
- РћРТвЂВВВВнокласснРСвЂВВВВРєРСвЂВВВВ
- Telegram
- РњРѕР№ Р В Р’В Р РЋРЎв„ўР В Р’В Р РЋРІР‚ВВВВРЎР‚
- LiveJournal
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Расчет сечения колонны по I варианту армирования 2 страница
4. Сопоставление значений
(Мul+Мuk)=68, 8кНм+ 97, 0кНм=165, 8кНм> > Мob=86, 1 кНм
показывает, что связевый ригель может воспринять, как продольный распор, так и дополнительную нагрузку от массы наружной стены.
5. Часть площади сечения нижней продольной арматуры, не требуемой для восприятия продольного распора, составляет:
Δ As=1, 168·10-3-8, 8·10-4=2, 88·10-4м2.
Величина момента, которую способно воспринять среднее сечение связевого ригеля, определится:
Δ Мul=Δ AsRs/(h0-xu/2)=2, 88·10-4·450000(0, 23-9, 05·10-2/2)=23, 9кНм
6. Сопоставим сумму опорного Мuk=68, 8кНм и пролетного
Δ Мul =23, 9кНм моментов с величиной балочного момента Мob=86, 1 кНм от дополнительной нагрузки.
Мul+Δ Мuk=68, 8кНм+ 23, 9кНм=92, 7кНм> Мob=86, 1 кНм
Рабочие армирование и принятая высота сечения обеспечивает восприятие дополнительных нагрузок, создаваемых массой наружной стены, на крайний связевый ригель.
7. Длину верхней рабочей арматуры от грани колонны в пролет можно определить:
Ls'=x0+l0n+bk+0, 15м для случая примыкания к угловой колонне.
Ls'=2(x0+l0n)+bk для случая примыкания к боковой колонне при одинаковой длине пролетов по обе стороны от колонны.
Здесь:
x0=- 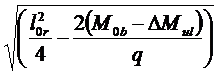 =3, 4-
=3, 4- 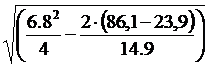 =1, 61м
=1, 61м
lon==(0, 50·450/14, 5 +8)·0, 018=0, 47м.
Таким образом:
для примыкания к угловой колонне длина верхних стержней определяется: (bk=0, 40м- ширина сечения колонны)
Ls/=x0+l0n+bk+0, 15м=1, 61+0, 47+0, 40+0, 15=2, 63м.
Длина верхних стержней, пропускаемых через боковую колонну в средний пролет ригеля, составляет:
Ls/=2(x0+l0n)+bk=2(1, 61+0, 47)+0, 40=4, 56м (по 2, 28м от оси колонны в смежные пролеты).
8. Аналогично, определив положение точки эпюры с величиной М=0 (на длине x0 от грани колонны в п. 7), можно определить длину нижних продольных стержней, обрываемых в пролете.
Подход по расчету и конструированию связевого ригеля, представленный в настоящем примере, может быть применен и для случая опирания на связевый ригель многопустотных плит смежной ячейки каркаса. Выступающая кверху часть связевого ригеля в пределах 4 см может быть размещена в цементной стяжке пола.
Пример 4
Расчет рабочего армирования монолитных несущих ригелей перекрытия с учетом действия в них продольного реактивно распора.
Трехпролетные неразрезные несущие ригеля выполнены с длиной пролетов по осям колонн 3l2 = 3x6. 20 м, размеры сетки колонн по осям 6. 20х6. 20 м. Ширина стенки монолитного таврового несущего ригеля bw1 = 0. 40м, полная высота сечения h = 0. 26 м, рабочая высота сечения h0 = 0. 23м. Высота сечения многопустотных плит h = 0. 22 м. Потолки плоские. Глубина размещения монолитных шпонок в полостях по торцам плит 0. 1м. Расчетная ширина сечения несущего крайнего ригеля bw = 0. 5 м, среднего – bw = 0. 6 м. Высота поперечного сечения связевых ригелей 0. 22 м, а ширина – 0, 50 м. Сечение железобетонных колонн 0. 4 x 0. 4 м, высота этажа hfl = 3. 0 м.
Бетон всех конструктивных элементов класса В25 (Rb = 14. 5 МПа, Rbt = 1. 05 МПа), рабочая арматура класса Ат500с (Rs = 450 МПа, Rsс = 400 МПа). Полная вертикальная расчетная нагрузка для I группы предельных состояний (по прочности) составляет g = 8. 4 кПа, в т. ч. постоянная и длительная gd = 6. 40 кПа.
Расчет
1. Продольный реактивный распор определяется:
- в крайних пролетах несущих ригелей по величине части временной нагрузки, составляющей разницу временной вертикальной нагрузки на соседние по высоте перекрытия многоэтажного здания, определяемую величиной снижения временной вертикальной нагрузки на перекрытие многоэтажного здания коэффициентом сочетаний ψ Ar определяемом согласно п. 3. 8 СНиП 2. 01. 07-85
- в средних пролетах несущих ригелей по полной величине расчетной вертикальной нагрузки на перекрытие за вычетом постоянной и длительной.
Грузовая площадь для нагрузки, приходящейся в крайнем пролете на средний несущий ригель, составляет Ac = l2xl1 = 6. 2 x 6. 2 = 38. 4 м2, для крайнего (бортового) несущего ригеля в том же пролете Ak = 0. 5× Ac = 19. 2 м2.
Величина снижения временной нагрузки определяется по величине коэффициента сочетаний ψ A (п. 3. 8 СНиП 2. 01. 07-85) для среднего ригеля:
ψ A1c = 0. 4 + = 0. 4 + = 0. 69;
для крайнего ригеля:
ψ A1k = 0. 4 + = 0. 81;
Пониженное значение полной вертикальной расчетной нагрузки на перекрытие в крайних пролетах несущего ригеля составляет:
для среднего ригеля gc’ = 6. 4 + 0. 69× 1. 5× 1. 3 = 7. 5 кПа;
для крайнего ригеля gk’ = 6. 4 + 0. 81× 1. 5× 1. 3 = 8. 0 кПа.
2. Значение изгибающего момента от действия расчетной нагрузки в расчетных сечениях несущих ригелей, определены упругим расчетом каркаса здания МКЭ (ППП “Stark-ES”) и представлены в таблице 1.
3. Площадь сечения рабочей арматуры класса А500с, предельная высота сжатой зоны и предельное усилие в расчетных сечениях, несущих ригелей, рассчитанные в соответствии со СНиП 2. 01. 03-84* по величине усилий от полной расчетной нагрузки, представленных в табл. 1, приведены в табл. 2.
Таблица 1
| Пролеты | Расположение расчетного сечения | Несущий ригель | Нагрузка | Обозначение усилия | Величина изгибаемого момента, кНм |
| крайний пролет | Середина пролета | крайний | полная | ML1 | 51. 6 |
| пониж., полная | ML1' | 49. 0 | |||
| постоянная | MLd1 | 39. 3 | |||
| средний | полная | ML2 | 79. 2 | ||
| пониж., полная | ML2' | 70. 6 | |||
| постоянная | MLd2 | 60. 3 | |||
| У крайней колонны | крайний | полная | M01k | -68. 2 | |
| пониж., полная | M0'1k | -64. 5 | |||
| постоянная | M0d1k | -52. 0 | |||
| средний | полная | M02k’ | -108. 3 | ||
| пониж., полная | M02k | -96. 3 | |||
| постоянная | M0d2k | -82. 5 | |||
| У средней колонны | крайний | полная | M01 | -76. 6 | |
| пониж., полная | M'01 | -72. 2 | |||
| постоянная | M0d1 | -58. 4 | |||
| средний | полная | M02 | -117. 1 | ||
| пониж., полная | M'02 | -104. 5 | |||
| постоянная | M0d2 | -89. 2 | |||
| средний пролет | У колонны | крайний | полная | M012 | -76. 6 |
| постоянная | M0d12 | -58. 4 | |||
| средний | полная | M022 | -117. 1 | ||
| постоянная | M0d22 | -89. 2 | |||
| В середине пролета | крайний | полная | ML21 | 48. 4 | |
| постоянная | MLd21 | 36. 9 | |||
| средний | полная | ML22 | 73. 8 | ||
| постоянная | MLd22 | 56. 2 |
Таблица 2
| Пролеты | Расположение расчетного сечения | Несущий ригель | Принятое сечение рабочей арматуры, м2 | Высота сжатой зоны Xu, м | Предельный момент Mu в расчетном сечении, кНм |
| крайний пролет | Середина пролета | крайний ригель | 5х12A500c | 3. 5х10-2 | 54. 0 |
| As = 5. 65х10-4 | |||||
| средний ригель | 2х20+2х 2 | 4. 4х10-2 | 79. 9 | ||
| As = 8. 54х10-4 | |||||
| У крайней колонны | крайний ригель | 2х20+1х 2 | 4. 6х10-2 | 69. 0 | |
| As = 7. 41х10-4 | |||||
| средний ригель | 2х25+3х 2 | 6. 8х10-2 | 116. 4 | ||
| As = 1. 32х10-3 | |||||
| У средней колонны | крайний ригель | 2х20+2х 2 | 5. 3х10-2 | 78. 2 | |
| As = 8. 54х10-4 | |||||
| средний ригель | 3х25+2х 2 | 8. 8х10-2 | 142. 2 | ||
| As = 1. 70х10-3 | |||||
| средний пролет | У колонны | крайний ригель | 2х20+2х 2 | 5. 3х10-2 | 78. 2 |
| As = 8. 54х10-4 | |||||
| средний ригель | 3х25+2х 2 | 8. 8х10-2 | 144. 2 | ||
| As = 1. 70х10-3 | |||||
| В середине пролета | крайний ригель | 5х 2 | 3. 5х10-2 | 54. 0 | |
| As = 5. 65х10-4 | |||||
| средний ригель | 2х20+2х 2 | 4. 4х10-2 | 79. 9 | ||
| As = 8. 54х10-4 |
4. Значение момента Mcrс, вызывающего образование вертикальных трещин в поперечных сечениях ригелей, определяется:
Mcrc = b1× Rbt× b× h2/3. 5
Коэффициент b1 = 1. 10 для крайнего ригеля и 1. 15 — для среднего, учитывающий включение в работу примыкающих многопустотных плит.
Величина Mcrc:
– для крайнего ригеля
Mcrc = 1. 10× 1050× 0. 50× 0. 262/3. 5 = 11. 2 кНм;
– для среднего ригеля
Mcrc = 1. 15× 1050× 0. 60× 0. 262/3. 5 = 14. 0 кНм;
5. Величина высоты " u" развития вертикальных трещин в расчетных сечениях ригелей при величинах характерных расчетных нагрузок, представленных в табл. 1, определяется:
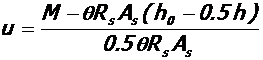 ,
,
где: M – величина изгибающего момента в расчетном сечении ригеля для рассматриваемого уровня нагрузки, 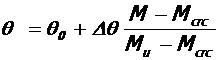 - коэффициент, учитывающий достигнутый уровень напряжений в рабочей арматуре для рассматриваемого уровня нагрузки;
- коэффициент, учитывающий достигнутый уровень напряжений в рабочей арматуре для рассматриваемого уровня нагрузки; 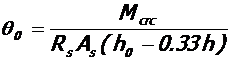 ;
;
Δ 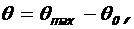
 ;
;
Rs и As - расчетное сопротивление растяжению и площадь сечения рабочей арматуры ригеля, h и h0 – соответственно полная и рабочая высота сечения ригеля; Mu, Xu и Mcrc - определены выше (табл. 2 и п. 4).
5. 1. Высота u трещины в середине крайнего пролета крайнего ригеля:
- при полной нагрузке:
M = Mu = 51, 6 кНм, Mu = 54, 0 кНм, Xu = 3, 5·10-2 м, As = 5, 65·10-4 м2.
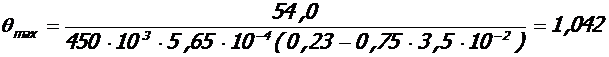 ;
;
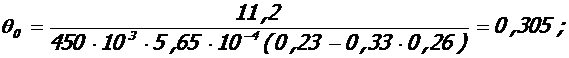
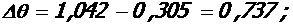
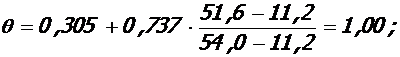
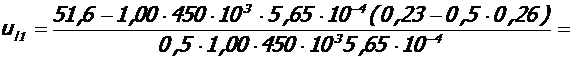 0. 206м;
0. 206м;
- при полной пониженной нагрузке:
M = 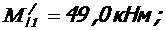
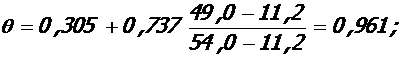
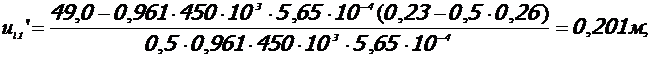
- при постоянной нагрузке:
М = 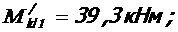
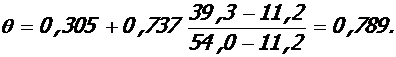
высоту трещины при постоянной нагрузке определять не требуется.
Аналогично расчет высоты u трещин, выполняют для всех расчетных сечений ригелей.
5. 2. Результаты расчета коэффициента 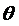 и высоты трещин u сведены в таблицу 3.
и высоты трещин u сведены в таблицу 3.
Таблица 3
| Пролеты | Расположение расчетного сечения | Несущий ригель | Нагрузка | Величина момента |М|, кНм | Значение коэффици-ента | Высота трещин | |
| обозна-чение | величи-на, м | ||||||
| К р а й н и й | Середина пролета | крайний | полная | 51, 6 | 1, 00 | Ul1 | 0, 206 |
| полная пониж. | 49, 0 | 0, 961 | U/ l1 | 0, 201 | |||
| постоянная | 39, 3 | 0, 789 | - | - | |||
| средний | полная | 79, 2 | 1, 047 | Ul2 | 0, 194 | ||
| полная пониж. | 70, 6 | 0, 964 | U/ l2 | 0, 192 | |||
| постоянная | 60, 3 | 0, 812 | - | - | |||
| У крайней колонны | крайний | полная | 68, 2 | 1, 047 | U01к | 0, 191 | |
| полная пониж. | 64, 5 | 0, 965 | U/ l1 | 0, 188 | |||
| постоянная | 52, 0 | 0, 815 | - | - | |||
| средний | полная | 108, 3 | 1, 021 | U02к | 0, 157 | ||
| полная пониж. | 96, 3 | 0, 940 | U/02к | 0, 156 | |||
| постоянная | 82, 5 | 0, 787 | - | - | |||
| У средней колонны | крайний | полная | 76, 6 | 1, 049 | U01 | 0, 180 | |
| полная пониж. | 72, 2 | 0, 966 | U/ 01 | 0, 178 | |||
| постоянная | 58, 4 | 0, 813 | - | - | |||
| средний | полная | 117, 1 | 1, 006 | U02 | 0, 127 | ||
| полная пониж. | 104, 5 | 0, 859 | U/ 02 | 0, 127 | |||
| постоянная | 89, 2 | 0, 717 | - | - | |||
| С р е д н и й | У колонн | крайний | полная | 76, 6 | 1, 049 | U012 | 0, 180 |
| постоянная | 58, 4 | 0, 813 | - | - | |||
| средний | полная | 117, 1 | 1, 096 | U022 | 0, 127 | ||
| постоянная | 89, 2 | 0, 717 | - | - | |||
| В середине пролета | крайний | полная | 48, 4 | 0, 990 | Ul12 | 0, 205 | |
| постоянная | 36, 9 | 0, 780 | - | - | |||
| средний | полная | 73, 8 | 1, 040 | Ul22 | 0, 190 | ||
| постоянная | 56, 2 | 0, 808 | - | - | |||
6. Средние относительные продольные деформации наиболее сжатой грани бетона ε bc и продольной рабочей арматуры ε st, (см. рис. 21 Указаний), а также среднее относительное удлинение продольной геометрической оси ε 0 несущих ригелей в расчетных сечениях определяют соответственно по формулам:
ε bc = ψ θ Rb / nЕb, ε st = ψ θ Rs / nЕs, где n=0, 85 - 0, 40 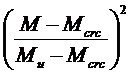 ;
;
ε 0 = (ε st - ω ε ε bc)/2; где, при распределенной нагрузке на ригель, ω ε = 0, 66 для сечений в середине пролета, ω ε = 0, 34 - для сечений у колонн.
6. 1. Сечения в середине крайнего пролета крайнего ригеля:
- при полной нагрузке:
М = 51, 6 кНм, θ = 1, 00, ψ b = 0, 9, ψ s = 0, 75,
ν = 0, 85 - 0, 40( 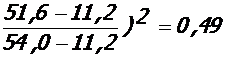 ;
;
ε bc = 0, 90·1, 0·14, 5/0, 49·30·103 = 8, 88·10-4;
ε st = 0, 75·1, 0·450/0, 49·200·103 = 3, 44·10-3;
ε 01l = (3, 44·10-3 - 0, 66·8, 88·10-4)/2 = 1, 43·10-3;
- при полной пониженной нагрузке:
М=49, 0 кНм; θ = 0, 961;
ν = 0, 85 - 0, 40 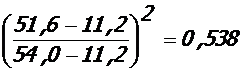 ;
;
ε bc = 0, 90·0, 961·14, 5/0, 538·30·103 = 7, 77·10-4;
ε st = 0, 75·0, 961·450/0, 538·200·103 = 3, 01·10-3;
ε 01l = (3, 01·10-3 - 0, 66·7, 77·10-4)/2 = 1, 25·10-3;
- при постоянной нагрузке:
М = 39, 3 кНм; θ = 0, 789;
ν = 0, 85 - 0, 40 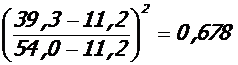 ;
;
ε bc = 0, 90·0, 789·450/0, 678·200·103 = 5, 06·10-4;
ε st = 0, 75·0, 789·450/0, 678·200·103 = 1, 96·10-3;
ε 01l = (1, 96·10-3 - 0, 66·5, 06·10-4)/2 = 8, 13·10-4.
6. 2. Результаты расчета деформаций сечений ригелей, выполненных аналогично п. 6. 1, сведены в табл. 4.
Таблица 4
| Про-ле т | Сечение | Нагрузка | Величина \М\, кНм | ν | Относительные деформации | |||
| от нагрузки | предельного | сжатой грани ригеля | рабочей растянутой арматуры | удлинения геометри-ческой оси | ||||
| К Р А Й Н И Й | середина пролета крайнего ригеля | полная | 51, 6 | 54, 0 | 0, 490 | 8, 88·10-4 | 3, 44·10-3 | 1, 43·10-3 |
| полная пониж. | 49, 0 | 54, 0 | 0, 538 | 7, 77·10-4 | 3, 01·10-3 | 1, 25·10-3 | ||
| постоянная | 39, 3 | 54, 0 | 0, 678 | 5, 06·10-4 | 1, 96·10-3 | 8, 13·10-4 | ||
| середина пролета среднего ригеля | полная | 79, 2 | 79, 9 | 0, 458 | 9, 93·10-4 | 3, 85·10-3 | 1, 60·10-3 | |
| полная пониж. | 70, 6 | 79, 9 | 0, 534 | 7, 86·10-4 | 3, 05·10-3 | 1, 26·10-3 | ||
| постоянная | 60, 3 | 79, 9 | 0, 652 | 5, 41·10-4 | 2, 10·10-3 | 8, 71·10-4 | ||
| у угловой колонны крайнего ригеля | полная | 68, 2 | 69, 0 | 0, 461 | 9, 88·10-4 | 3, 83·10-3 | 1, 75·10-3 | |
| полная пониж. | 64, 5 | 69, 0 | 0, 535 | 7, 85·10-4 | 3, 04·10-3 | 1, 39·10-3 | ||
| постоянная | 52, 0 | 69, 0 | 0, 651 | 5, 45·10-4 | 2, 11·10-3 | 1, 15·10-3 | ||
| у крайней колонны среднего ригеля | полная | 108, 3 | 116, 4 | 0, 511 | 8, 69·10-4 | 3, 37·10-3 | 1, 54·10-3 | |
| полная пониж. | 96, 3 | 116, 4 | 0, 572 | 7, 15·10-4 | 2, 77·10-3 | 1, 26·10-3 | ||
| постоянная | 82, 5 | 116, 4 | 0, 671 | 5, 10·10-4 | 2, 36·10-3 | 1, 10·10-3 | ||
| у средней колонны крайнего ригеля | полная | 76, 6 | 78, 2 | 0, 469 | 9, 73·10-4 | 3, 78·10-3 | 1, 72·10-3 | |
| полная пониж. | 72, 2 | 78, 2 | 0, 498 | 8, 44·10-4 | 3, 27·10-3 | 1, 49·10-3 | ||
| постоянная | 58, 4 | 78, 2 | 0, 651 | 5, 43·10-4 | 2, 11·10-3 | 9, 61·10-4 | ||
| у средней колонны среднего ригеля | полная | 117, 1 | 142, 2 | 0, 591 | 7, 40·10-4 | 2, 87·10-3 | 1, 31·10-3 | |
| полная пониж. | 104, 5 | 142, 2 | 0, 640 | 5, 84·10-4 | 2, 26·10-3 | 1, 03·10-3 | ||
| постоянная | 89, 2 | 0, 712 | 4, 38·10-4 | 1, 70·10-3 | 7, 75·10-4 | |||
| С Р Е Д Н И Й | крайний ригель у колонны | полная | 76, 6 | 78, 2 | 0, 469 | 9, 73·10-4 | 3, 78·10-3 | 1, 72·10-3 |
| постоянная | 58, 4 | 0, 651 | 5, 43·10-4 | 2, 11·10-4 | 9, 61·10-4 | |||
| средний ригель у колонны | полная | 117, 1 | 142, 2 | 0, 591 | 7, 40·10-4 | 2, 87·10-3 | 1, 31·10-3 | |
| постоянная | 89, 2 | 0, 712 | 4, 38·10-4 | 1, 70·10-3 | 7, 75·10-4 | |||
| крайний ригель в середине пролета | полная | 48, 4 | 54, 0 | 0, 548 | 7, 86·10-4 | 3, 05·10-3 | 1, 26·10-3 | |
| постоянная | 36, 9 | 0, 716 | 4, 74·10-4 | 1, 84·10-3 | 7, 63·10-4 | |||
| средний ригель в середине пролета | полная | 73, 8 | 79, 9 | 0, 521 | 8, 68·10-4 | 3, 37·10-3 | 1, 40·10-3 | |
| постоянная | 56, 0 | 0, 688 | 5, 11·10-4 | 1, 98·10-3 | 8, 23·10-4 | |||
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|