№34 Види складних суджень. №35 Табличне значення логічних сполучників

№34 Види складних суджень

Складним називається судження, яке складається з двох або більше простих суджень з'єднаних за

допомогою логічних сполучників. Наприклад, «Моя сестра навчається у консерваторії, а брат — в університеті». За типом логічних сполучників складні судження поділяються на: а) з'єднувальні; б) роз’єднувальні; в) умовні; г) еквівалентні. Складні судження поділяють на: — порівнювані; — непорівнювані. Порівнюваними називають складні судження, які складаються з одних і тих же простих суджень, але різняться логічними термінами. Наприклад, А & В і А ↔ В тощо.

Непорівнюваними називаються складні судження, в яких хоча б одне просте судження не співпадає.

Наприклад, A & C і А ↔ В тощо. Серед порівнюваних суджень виділяють: — сумісні; — несумісні.

Сумісними називаються складні судження, які при однакових наборах значень простих можуть бути

істинними. Несумісними називаються складні судження, які при однакових наборах значень простих не можуть бути разом істинними.

№35 Табличне значення логічних сполучників

Логічні сполучники фіксують зв'язки між висловлюваннями. Символи для позначення логічних сполучників: «і» — кон'юнкція (& ); «або» — диз'юнкція (V); «якщо, то» — імплікація (→ ); «якщо і тільки якщо, то» — еквівалентність (↔ ); «ні» — заперечення (—). Запереченням називається логічна операція, за допомогою якої з певного істинного висловлювання отримують нове висловлювання, яке буде хибним, і навпаки. Побудуємо таблицю істинності для заперечення:

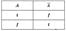
Кон'юнкцією називається складне висловлювання (А & В), яке істинне тоді і тільки тоді, коли істинне А і істинне В. Наприклад, висловлювання «Ми знаходилися в аудиторії, і на вулиці йшов дощ» буде істинним лише тоді, коли істинними будуть обидва прості висловлювання. Наведеному визначенню кон'юнкції відповідає така таблиця істинності:

Диз'юнкція – це складне висловлювання, утворене за допомогою сполучника «або», відображає існування різних можливостей. Це висловлювання буде істинним, якщо одна з двох можливостей

реалізується. Істинним воно буде і тоді, коли реалізуються обидві можливості. Наприклад, висловлювання «Він досяг гарних результатів у навчанні або завдяки старанності, або завдяки

здібностям» відображає наявність різних можливостей отримання гарних результатів у навчанні. У природній мові аналогами диз'юнкції є вирази: «А або В», «А або В, або обидва», «А і або В», «А, якщо не В». Різні значення сполучника «або» у логіці фіксуються: — з'єднувальною диз'юнкцією (або просто диз'юнкцією); — розділовою диз'юнкцією (або суворою диз'юнкцією); — виключною диз'юнкцією (або антикон'юнкцією). З'єднувальною диз'юнкцією називають складне висловлювання А V В, яке буде істинним тоді і тільки тоді, коли буде істинним хоча б одне з висловлювань А або В. Наведення визначення відображене у таблиці істинності для диз'юнкції:

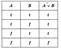
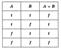
Сильною диз'юнкцією називається висловлювання А V В, яке істинне тоді і тільки тоді, коли одне з

простих висловлювань, що входять до його складу, істинне, а друге — обов'язково хибне. Наприклад, «Ця людина або житель Києва, або іногородній». Таблиця істинності для сильної диз'юнкції має

такий вигляд:

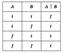
Виключенням ( антикон'юнкцією ) називають складне висловлювання, яке істинне тоді і тільки тоді,

коли у крайньому разі одне з простих висловлювань, що його складають, хибне. Наприклад, «Він є студентом або школярем». Цьому визначенню виключення відповідає таблиця істинності:

Граматичному сполучнику «якщо, то» відповідає логічний термін « імплікація ». Висловлювання, якому надіслане слово «якщо» і яке стоїть перед словом «то», називають антецедентом. Висловлювання, яке стоїть після слова «то», називають консеквентом. Для імплікації характерна та обставина, що ні в якому разі не може трапитися так, щоб антецедент був істинним, а консеквент — хибним. Це відображено в таблиці істинності для імплікації:

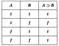
Еквіваленція (або подвійна імплікація) висловлювань А і В — це складне висловлювання, яке буде істинним тоді і тоді, коли А і В одночасно істинні або одночасно хибні. В інших випадках еквіваленція буде хибною. Еквіваленція виражає відношення між достатньою і необхідною умовою та її наслідком. Напрклад, «Якщо він знає англійську мову, то він перекладе цей текст». У природній мові аналогами еквіваленції є вирази: «А тоді і тільки тоді, коли В», «А якщо В і В якщо А», «Для А достатньо і необхідно В», «А матеріально еквівалентно В». Наведеному визначенню еквіваленції відповідає така таблиця істинності:

⇐ Предыдущая 17 18 19 20 212223 24 25 26 Следующая ⇒