
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
6. Стоячие волны бесконечной глубины.
6. Стоячие волны бесконечной глубины.
Встречаются случаи редко, когда наблюдаются стоячие волны. Узлы стоят на месте, чтобы волны были расположены так нужно подобрать постоянные интегрирования в функции « »
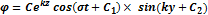
Запишем уравнение свободной поверхности:
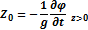
Возьмем производную 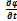 :
:
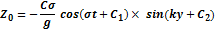
Возьмем начало, чтобы при t = 0, y =0, z =0, т. е. первый узел лежит в начале координат. Тогда cos C1= 0. Отсюда С 2= 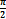
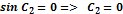
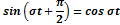
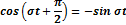
...
Скорость частицы I
В данном случае мы будем рассматривать скорость частицы по составленной y и z
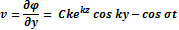
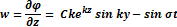
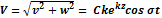
При t = 0, 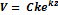
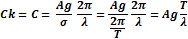
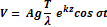
Отсюда видно, что скорость частицы в стоячей волне зависит от Y, значит, что все частицы на волне движутся с одной и той же скоростью независимо от положения. Дифференциальные уравнения траектории частицы выглядит следующим образом:
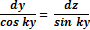
Найдем наклон линий тока:
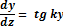
Сравним размах колебаний на поверхности и глубинах:
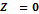
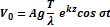
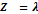
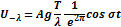
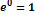
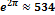
Стоячие волны являются поверхностными волнами, т. к. на глубине равной длине волны, скорость частицы убывает в 534 раза, соответственно колебаний на глубине не существует:
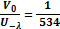
7. Прогрессивные волны бесконечной глубины
Прогрессивные волны – это такие волны, в которых характерные точки формы волны (гребни, узлы, и впадины) перемещаются.
Рассмотрим два движения:
1) 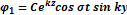
2) 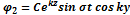
Возможно, что их супер позиция приведет к движению волны.
Вторая волна так-же является стоячей, только фаза сдвинута на четверть периода.
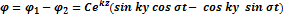
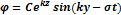
Определим свободную поверхность:
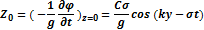
Таким образом, мы получим потенциал и уравнение свободной поверхности для прогрессивных волн.
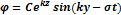
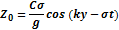
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|