
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
2. Связь между метеорологическими производными
2. Связь между метеорологическими производными
Индивидуальная производная описывает изменение некоторого свойства f в индивидуальной частице воздуха с течением времени. Индивидуальная производная является полной производной функции f(x, y, z, t) по времени, т. е..
Локальная производная описывает изменения во времени некоторого
свойства f в неподвижной (фиксированной) точке пространства. Локальная производная характеризуется частной производной функции f(x, y, z, t) по  времени, т. е.
времени, т. е.
 на описывает изменения элемента в данной точке поля.
на описывает изменения элемента в данной точке поля.
Геометрическая производная характеризует изменения свойства f в
пространстве или в данном направлении. Она является частной производной



 функции f(x, y, z, t) по направлению, т. е.
функции f(x, y, z, t) по направлению, т. е.
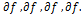

Оператор Эйлера
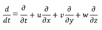
 Здесь 𝛿 𝑓 = 𝑓 2 − 𝑓 1 и 𝛿 𝑥 = 𝑥 2 − 𝑥 1 – конечные приращения функции f и независимой переменной x. (рисунок 2. 1).
Здесь 𝛿 𝑓 = 𝑓 2 − 𝑓 1 и 𝛿 𝑥 = 𝑥 2 − 𝑥 1 – конечные приращения функции f и независимой переменной x. (рисунок 2. 1).
Таким образом, в данном случае отношение дифференциалов заменяется отношением конечных разностей.
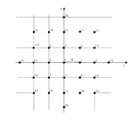
Для определения производных, осредненных по некоторой траектории, используют систему равноотстоящих точек (узлов), которые в совокупности образуют расчетную сетку. Расстояние между соседними узлами называют шагом сетки и обозначают d.
Формулы для определения производных выглядят таким образом:
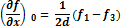
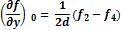
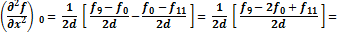
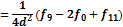
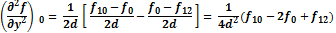
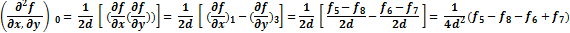
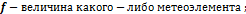

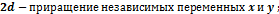
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|