
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
3. Волновые движения в атмосфере.
3. Волновые движения в атмосфере.
Крупномасштабные волны – это проявление инерционных сил. Волны этого класса иногда называют инерционными, а также длинными волнами, волнами Россби. Они возможны лишь на вращающейся Земле. Волны этого класса имеют длину до нескольких тысяч километров, скорость – до десятков метров в секунду, период – до нескольких суток. Их амплитуда оказывается значительной и составляет, например, в поле давления 20-100 гПа. Например, волны Россби
Гравитационные волны связаны с проявлением силы тяжести, то есть с влиянием гравитационного поля Земли. Периоды колебаний, связанных с гравитационными волнами в атмосфере, составляют около 330 с, а скорость перемещения этих волн изменяется от десятков до сотен м/с, достигая в отдельных случаях 300 м/с.
Акустические волны, или волны сжатия, обусловлены сжатием или разрежением среды. Период колебаний этих волн не превышает 300 с. Так как к этому классу относятся и волны, воспринимаемые органами слуха человека (с частотой от 20 до 20 000 Гц), то эти волны называют также звуковыми
Скорость перемещения акустических волн велика и колеблется около 300 м/с (скорость звуковых волн, воспринимаемых органами слуха человека в сухой атмосфере, составляет около 330 м/с).
4. Гравитационные волны на свободной поверхности несжимаемой жидкости.
Рассмотрим сначала простейший случай волнового движения на свободной поверхности слоя несжимаемой жидкости толщиной h, простирающегося по горизонтали во все стороны неограниченно.
Жидкость, которая в начальный момент имеет горизонтальную поверхность. Возникновение волны происходит, если в некотором месте прикладывается импульс, т. е. возникает давление.
Таким образом, возникновение волны связано с импульсным повышением давления.
𝛿 𝑡
I = ∑ 𝑝 𝑑 𝑡
dt – малый промежуток времени
I – импульс – это мгновенное действие большого давления
Сделаем допущения:
1) Жидкость несжимаема (r=const)
2) Жидкость идеальная (без трения) N = 0
3) Массовая сила есть сила потенциальная (сила геопотенциала) 𝐹 ̅ = 𝑔 ̅
скорость частицы, вызванная импульсом силы, будет равна:
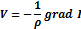
Для отыскания функции j мы можем воспользоваться уравнением Коши–Лагранжа, которое справедливо для безвихревого (потенциального) движения.
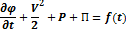
Нужно сделать некоторые упрощающие предположения, т. к. в общем виде задача не может быть решена:
1) Ускорение свободного падения – величина постоянная
2) Плотность - величина постоянная
3) Квадрат скорости равен нулю
Тогда уравнение Коши-Лангранжа будет иметь такой вид:
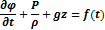
Теперь нужно определить j. Это можно сделать из уравнения неразрывности.
Уравнение неразрывности выражает условия сохранения массы, т. е. тот факт, что если в данном бесконечно малом объеме втекание и истечение жидкости не равны, то происходит изменение массы, что невозможно.
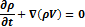
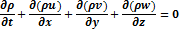
Так как r=const, то уравнение неразрывности будет:
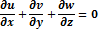
Или
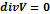
Подставим: 𝑢 = 𝜕 𝜑; 𝑣 = 𝜕 𝜑; 𝑤 = 𝜕 𝜑
Получим: Оператор Лапласа
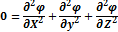
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|