
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Куттии одї. Божественная Коробка
Куттии одї
 : Аз «ќутти одї» якбора -то элемент гирифта мешавад.
: Аз «ќутти одї» якбора -то элемент гирифта мешавад.
 : Последователно извлекаем элементы из обычной коробки, и получаем на выходе определенную кучку из -элементов. И нам очень важен порядок извлекаемых объектов.
: Последователно извлекаем элементы из обычной коробки, и получаем на выходе определенную кучку из -элементов. И нам очень важен порядок извлекаемых объектов.
Мы рассмотрели все варианты обычной коробки. Надо добавить, что когда мы рассмотрели вариантов обычной коробки, у нас количество элементов было 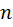 -штук. Свойство божественной коробки отличается от свойство обычной коробки. Разница в том, что в божественной коробки не содержится
-штук. Свойство божественной коробки отличается от свойство обычной коробки. Разница в том, что в божественной коробки не содержится 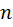 -элементов, а содержится бесчисленное множество элементов, и все виды элементы божественной коробки совпадают с элементами обычной коробки. Божественная коробка содержит бесчисленное множество карточек. Т. е есть бесчисленное множество карточек на которых нарисовано элемент
-элементов, а содержится бесчисленное множество элементов, и все виды элементы божественной коробки совпадают с элементами обычной коробки. Божественная коробка содержит бесчисленное множество карточек. Т. е есть бесчисленное множество карточек на которых нарисовано элемент 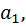 есть бесчисленное множество карточек на которых нарисовано элемент
есть бесчисленное множество карточек на которых нарисовано элемент 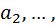 есть бесчисленное множество карточек на которых нарисовано элемент
есть бесчисленное множество карточек на которых нарисовано элемент  То есть у нас есть
То есть у нас есть 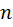 -бесчисленных множеств, и все они запихнуты в эту божественную коробку. Давайте начнем рассмотреть два варианта божественной коробки.
-бесчисленных множеств, и все они запихнуты в эту божественную коробку. Давайте начнем рассмотреть два варианта божественной коробки.
Божественная Коробка
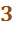 Вариант: Зачерпываем в пригоршни
Вариант: Зачерпываем в пригоршни  -элементов из божественной коробки.
-элементов из божественной коробки.
 Вариант: Последователно извлекаем элементы из божественной коробки, и получаем на выходе определенную кучку из
Вариант: Последователно извлекаем элементы из божественной коробки, и получаем на выходе определенную кучку из  -элементов. И нам очень важен порядок извлекаемых объектов.
-элементов. И нам очень важен порядок извлекаемых объектов.
И так мы рассмотрели всех вариантов. Теперь каждому варианту даем определенное название.
 Вариант:
Вариант:  -сочетания без повторений
-сочетания без повторений 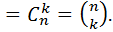
 Вариант:
Вариант:  -размещения без повторений
-размещения без повторений 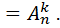
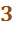 Вариант:
Вариант:  -сочетания с повторениями
-сочетания с повторениями 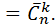
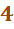 Вариант:
Вариант:  -размещения с повторениями
-размещения с повторениями 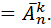
Теорема: 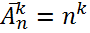 .
.
Доказательство: 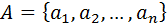 . На первую позицию в будущем
. На первую позицию в будущем  -размещении с повторениями, мы можем выбрать любой из этих
-размещении с повторениями, мы можем выбрать любой из этих
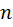 -объектов. На вторую позицию в
-объектов. На вторую позицию в  -размещении мы тоже можем выбрать любой из наших
-размещении мы тоже можем выбрать любой из наших 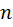 -объектов. …. На
-объектов. …. На  -ю позицию мы тоже можем выбрать любой из наших
-ю позицию мы тоже можем выбрать любой из наших 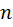 -объектов. Но понятное дело, что количество таких размещений с повторениями и будем вычислять как:
-объектов. Но понятное дело, что количество таких размещений с повторениями и будем вычислять как:
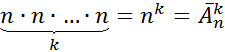 . ЧТД.
. ЧТД.
Теорема: 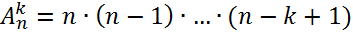 .
.
Доказательство: На первую позицию в  -размещений без повторений мы можем выбрать любой из
-размещений без повторений мы можем выбрать любой из 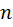 -объектов. На вторую позицию в
-объектов. На вторую позицию в
 -размещений без повторений мы можем выбрать любой из освщихся
-размещений без повторений мы можем выбрать любой из освщихся
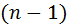 -объектов. ... . На
-объектов. ... . На  -ю позицию в
-ю позицию в 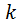 -размещений без повторений мы можем выбрать любой из оставщихся
-размещений без повторений мы можем выбрать любой из оставщихся 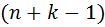 -объектов. По правилу умножения
-объектов. По правилу умножения 
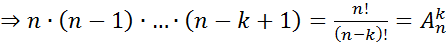 . ЧТД.
. ЧТД.
Следствие: 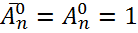 .
.
Доказательство: Ну почему это так? – Это -размещений мы нечего не размещаем мы просто нечего незделаем. Но сколькими способами можно выташить так сказать пустое множество объектов? - И понятное дело, что можно сделать способом. И даже, если в формулах поставить будет тоже верно, то есть ЧТД.
Следствие:  ;
;
 (Число перестановок ).
(Число перестановок ).
Доказательство: Что значит выбрать -объектов из множество мощности 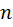 ?. Что значит выбрать с учетом последовательности, с учетом порядка? Ну нашы формулы нам дают следующее:
?. Что значит выбрать с учетом последовательности, с учетом порядка? Ну нашы формулы нам дают следующее:
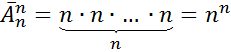 ;
;
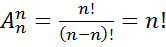 ( число различных всевозможных перестановок ). ЧТД.
( число различных всевозможных перестановок ). ЧТД.
Задача: На пиратском корабле есть 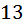 человек экипажа. Сколько существует различных способов выбрать из этих
человек экипажа. Сколько существует различных способов выбрать из этих 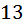 человек капитана и боцмана ему в помощнике?
человек капитана и боцмана ему в помощнике?
Решение: Давайте обозначим людей как 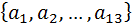 . Из этого множество из
. Из этого множество из 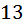 объектов нам нужно выбрать два объекта без повторений. И здесь при выборе объектов речь идёт о размещении, так как нам важен порядок следований объектов внутри нашей пары которую мы выбираем. То есть это должны быть два разных объекта, и порядок их нам важен, потому, что важно какие именно должности эти два товарищи будут иметь – кто из них капитан, а кто из них боцман. Поэтому это в чистом виде два размещения без повторений из
объектов нам нужно выбрать два объекта без повторений. И здесь при выборе объектов речь идёт о размещении, так как нам важен порядок следований объектов внутри нашей пары которую мы выбираем. То есть это должны быть два разных объекта, и порядок их нам важен, потому, что важно какие именно должности эти два товарищи будут иметь – кто из них капитан, а кто из них боцман. Поэтому это в чистом виде два размещения без повторений из 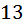 объектов, то есть
объектов, то есть 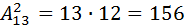 различных способов составить из
различных способов составить из 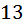 член экипажа пару капитана и боцмана.
член экипажа пару капитана и боцмана.
Ответ: 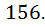
Задача: Имеется игрушечный поезд. Он состоит из 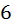 вагонов. А в наборе к этому игрушечному поезду имеется
вагонов. А в наборе к этому игрушечному поезду имеется 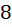 типов вагонов ( плацкартные, купейные, ресторан, … ).
типов вагонов ( плацкартные, купейные, ресторан, … ).
а) Сколько всего существует способов составить поезд, если все вагоны в этом поезде были разными?
б) Сколько есть способов составить поезд, если все вагоны в этом поезде были различными и в этом поезде обязательно есть вагон ресторан?
Решение:
а)Мы должны составить поезд из 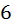 вагонов. И здесь у нас речь идёт о выборе. Ну понятное дело, мы выбираем из множество который состоит из
вагонов. И здесь у нас речь идёт о выборе. Ну понятное дело, мы выбираем из множество который состоит из 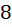 элементов( вагонов )
элементов( вагонов )  . И надо выбрать их ровно
. И надо выбрать их ровно 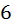 штук из этой множестве который состоит из
штук из этой множестве который состоит из 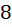 элементов, и все вагоны должны быть разными. Значить наш выбор – это размещение без повторение, то есть
элементов, и все вагоны должны быть разными. Значить наш выбор – это размещение без повторение, то есть  способов.
способов.
б) Выбираем позицию для вагонов ресторан. Это естественно делается шестью способами. После чего у нас остается 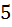 позиций. И из
позиций. И из 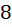 типов вагонов который у нас были в нашем распоряжении, остаётся только семь типов вагонов которыми можно пользоваться. Следовательно количество способов который нам нужен, равен
типов вагонов который у нас были в нашем распоряжении, остаётся только семь типов вагонов которыми можно пользоваться. Следовательно количество способов который нам нужен, равен  ;
;
Ответ:  .
.
Задача: Маша и Петя подумали некий язык, в котором символы, , .
а) Сколько существует различных слов из пяти букв?
б) Сколько можно составить слов, у которых длина не больше пяти?
в) Сколько можно составить слов из не более пяти букв, если первая буква – эта обязательно ?
Решение:
а) Понятно, что речь идет о повторении. То есть три объекта, и из них мы выбираем какие то угодно 5, при этом возможно повтор  различных слов из пяти букв которое можно составить на языке Маши и Пети;
различных слов из пяти букв которое можно составить на языке Маши и Пети;
б) Мы уже знаем сколько есть слов каждый из которых состоит из ровно пяти букв – эта 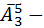 слов; Дальше мы можем совершенно аналогично посчитать количество слов в каждом из которых ровно четыре буквы – эта
слов; Дальше мы можем совершенно аналогично посчитать количество слов в каждом из которых ровно четыре буквы – эта 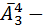 слов. Дальше мы посмотрим на слова которые содержат всего три буквы – эта
слов. Дальше мы посмотрим на слова которые содержат всего три буквы – эта 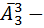 слов; Посмотрим две буквы – эта
слов; Посмотрим две буквы – эта 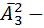 слов. И наконец одна буква– эта
слов. И наконец одна буква– эта 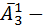 слов. Значить количество слов длина которых не более пяти букв, равен
слов. Значить количество слов длина которых не более пяти букв, равен 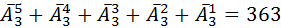 слов.
слов.
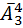 способами. Дальше найдем количество слов длины четыре – эта аналогичным образом будет
способами. Дальше найдем количество слов длины четыре – эта аналогичным образом будет  слов. Дальше найдем количество слов длины три – эта сделается
слов. Дальше найдем количество слов длины три – эта сделается 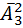 способами. Дальше количество слов длины два – эта
способами. Дальше количество слов длины два – эта 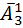 способов. И наконец количество слов длины один – эта делается
способов. И наконец количество слов длины один – эта делается 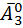 способами.
способами. 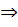 Итого мы получим
Итого мы получим 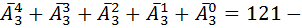 количество слов которые не более пяти букв имеют в своем записи, и первая буква которых .
количество слов которые не более пяти букв имеют в своем записи, и первая буква которых . 
Задача: Есть три студента – Амина, Марям и Салва. Они собираются на свадьбу. Им необходимо нарядится. И у них есть в распоряжении некоторые количество разных нарядов – 4рубашки, 3джинсы, и 8пар обуви. Сколькими способами они могут распределить между собой эти самые наряды, так чтобы по-разному нарядиться для свадьбы?
Решение: Давайте сначала рассмотрим рубашки, и обозначим их как  Из этих четырех объектов надо выбрать три распределяя по разным студентам. Ну естественно – три размещения без повторений, потому что порядок исключительно важен и рубашки все разные. То есть количество способов раздачи рубашек – эта
Из этих четырех объектов надо выбрать три распределяя по разным студентам. Ну естественно – три размещения без повторений, потому что порядок исключительно важен и рубашки все разные. То есть количество способов раздачи рубашек – эта 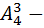 способов. И тоже самое касается ситуации с раздачи джинсы –
способов. И тоже самое касается ситуации с раздачи джинсы – 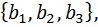 то есть
то есть  способов. И тоже самое с ситуации которое касается пар обуви –
способов. И тоже самое с ситуации которое касается пар обуви – 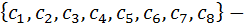 это сделается
это сделается 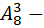 способами. Итого по правилу умножения получается, что количество способов распределения между студентами эти самые наряды, так чтобы по-разному нарядиться для свадьбы равен
способами. Итого по правилу умножения получается, что количество способов распределения между студентами эти самые наряды, так чтобы по-разному нарядиться для свадьбы равен 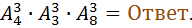
Теорема: 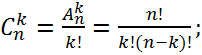
Доказательство: Пусь у нас есть множество состоящий из 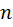 -объектов
-объектов 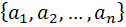 . Из этого множество мы извлекаем всевозможные
. Из этого множество мы извлекаем всевозможные  -сочетаний без повторений. Берём какой ни будь
-сочетаний без повторений. Берём какой ни будь 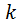 -сочетаний без повторений. Нарисуем его как прямоугольник, и рядом пищем элементы этой сочетаний, а внутри пищем номер данной сочетаний:
-сочетаний без повторений. Нарисуем его как прямоугольник, и рядом пищем элементы этой сочетаний, а внутри пищем номер данной сочетаний:
| 1 |
{ 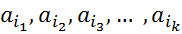 }
}
(множество элементов этой конкретной сочетаний)
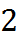
|
 -сочетаний возмë м:
-сочетаний возмë м:
{ 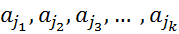 }
}
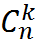
|

{  }
}
Последний прямоугольник ( наш  -сочетаний без повторений ) имеет номер
-сочетаний без повторений ) имеет номер 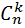 , так как все эти прямоугольники показывают количеству всех конкретных
, так как все эти прямоугольники показывают количеству всех конкретных  -сочетаний без повторений. И номер всех сочетаний –это и есть количество всех возможных
-сочетаний без повторений. И номер всех сочетаний –это и есть количество всех возможных  -сочетаний, то есть равен номеру последней прямоугольника. Теперь элемент каждого прямоугольника переставляем. И это у каждого прямоугольника
-сочетаний, то есть равен номеру последней прямоугольника. Теперь элемент каждого прямоугольника переставляем. И это у каждого прямоугольника 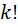 –различных размещений отвечающих данному сочетанию. А сколько всего размещений? – Очевидно, что всего
–различных размещений отвечающих данному сочетанию. А сколько всего размещений? – Очевидно, что всего 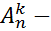 размещений. То есть получается
размещений. То есть получается 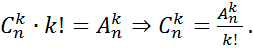
ЧТД.
Теорема: 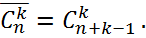
Доказательство: Пусть у нас есть какой-то набор объектов { 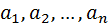 }. Из этих объектов мы составляем всевозможные
}. Из этих объектов мы составляем всевозможные 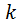 -сочетания с повторениями. Каждому из этих
-сочетания с повторениями. Каждому из этих  -сочетаний с повторениями мы сопоставляем паспорт с номером
-сочетаний с повторениями мы сопоставляем паспорт с номером 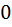 и
и 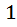 , другими словами мы закодируем наш паспорт. Мы просто рисуем в начале столько единиц, сколько раз в данном конкретном
, другими словами мы закодируем наш паспорт. Мы просто рисуем в начале столько единиц, сколько раз в данном конкретном  -сочетании встречается элемент
-сочетании встречается элемент 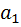 :
: 
И не рисуем единицы вовсе, если 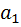 в данном конкретном
в данном конкретном  -сочетаний ( которое мы пытаемся закодировать ) просто не встречается. Дальше рисуем перегородку в виде
-сочетаний ( которое мы пытаемся закодировать ) просто не встречается. Дальше рисуем перегородку в виде 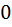 отделяющего встречаемого элемента
отделяющего встречаемого элемента 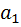 от встречаемого символа
от встречаемого символа 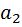 :
:
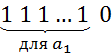
И рисуем столько единиц, сколько раз встречается 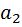 :
:
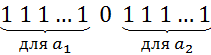
И снова рисуем 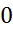 :
:
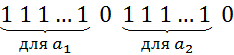
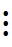
И в конце единицы (если возможно):
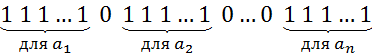
То есть мы взяли  -сочетаний с повторениями. Посмотрели сколько раз
-сочетаний с повторениями. Посмотрели сколько раз 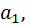 сколько раз
сколько раз 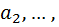 сколько раз
сколько раз 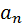 встречается, и нарисовали соответствующие единиц, то есть количество единиц. А эти количество единиц разделили перегородками нулями. У нас каждому
встречается, и нарисовали соответствующие единиц, то есть количество единиц. А эти количество единиц разделили перегородками нулями. У нас каждому  -сочетанию с повторениями отвечает уникальный паспорт – такая последовательность из единицы и нулей в которой
-сочетанию с повторениями отвечает уникальный паспорт – такая последовательность из единицы и нулей в которой  -штук единиц, а перегородок
-штук единиц, а перегородок 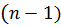 -штук. Значит наши паспорта – это различные последовательности из
-штук. Значит наши паспорта – это различные последовательности из 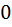 и
и 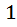 , в каждой из которых ровно
, в каждой из которых ровно  -единиц и ровно
-единиц и ровно 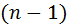 -нулей, и длина всей последовательности-это
-нулей, и длина всей последовательности-это  И вот нас интересует сколько всего бывает таких последовательностей. Давайте посчитаем количество последовательностей. Это количество равно количеству способов выбрать
И вот нас интересует сколько всего бывает таких последовательностей. Давайте посчитаем количество последовательностей. Это количество равно количеству способов выбрать  -позиций из
-позиций из 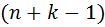 возможных позиций для постановки на эти
возможных позиций для постановки на эти  -позиций единицы, то есть
-позиций единицы, то есть 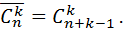

Задача: Есть некая лаборатория – медицинская. И в этой лаборатории имеется 10-подопытных мышей, и все они разные. Надо выбрать пять мышей из этих десяти, так чтобы над ними поставить эксперимент. Сколько есть способов выбрать пять мышей для эксперимента?
Решение: Понятно, что у нас имеется множество состоящий из десяти различных объектов – эта вот эти самые наши десять мышей– 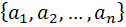 . И из этого множество мы извлекаем пять штук мышей – естественно разных, поэтому речь идет об извлечении 5–сочетания без повторений. Здесь наше извлечение–эта не пять размещений, а точно 5–сочетаний, потому что ни как в рамках постановки вопроса, не оговорена в каком порядке над этими мышами будет производится эксперимент. Следовательно
. И из этого множество мы извлекаем пять штук мышей – естественно разных, поэтому речь идет об извлечении 5–сочетания без повторений. Здесь наше извлечение–эта не пять размещений, а точно 5–сочетаний, потому что ни как в рамках постановки вопроса, не оговорена в каком порядке над этими мышами будет производится эксперимент. Следовательно 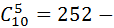 способов выбрать пять мышей для эксперимента.
способов выбрать пять мышей для эксперимента. 
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|