1.3 Принсип Дирихле

Определение: Есть 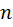ящиков и 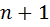кроликов. Как не рассаживай кроликов по ящикам, найдется ящик в котором хотя бы 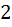кроликов.

Пример : У нас есть квадрат со стороной 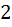, и в этом квадрате берём 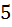точек. Как бы 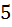точек ни были расположены внутри квадрата со стороной 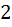, найдутся два из них на расстоянии .

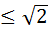Решение: Давайте перерисуем квадрат со стороной 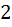, и разобьём его на 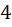клеточки ( ящиков ) со стороной 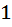. Тогда получиться, что как ни бросай 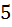точек ( кроликов ) по клеточкам ( ящикам ), обязательно найдется хотя бы одна клеточка в которую попадает не меньше 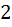точек ( кроликов ). А если 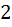точки попадали внутрь одной клетки, то конечно расстояние между ними не превосходит длины диагонали этой клетки, потому что диагональ-это самое большое расстояние внутри клетки. Ну а длина диагонали по теореме Пифагора . То есть получается, что те две точки которые мы нашли в нашей клеточки ( в нашем ящике) – они удалены друг от друга на расстоянии не превосходящее .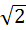

2 2

Масъала: Тангањои 1дирама, 2дирама, 5дирама ва 10дирама њастанд. Миќдори минималии чунин тангањо ёфта шавад, ки дар байни онњо 6 тангаи ќурбаш якхела бошад?

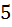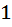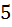Решение: Действително мы можем взять монет достоинством дир, монет достоинством 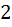дир, 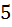монет достоинством 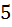дир, и, 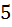монет достоинством 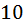дир. При этом в сумме получается, 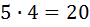монет, и среди них нет шестёрки одинаковых. Но нам необходимо и достаточно взять так чтобы с гарантией среди взятых монет нашлось 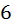монет одного достоинство. Это означает, что либо монет с достоинством 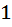дир не меньше шести, либо монет с достоинством 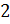дир не меньше шести, либо монет с достоинством 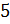дир не меньше шести, и либо монет с достоинством 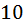дир не меньше шести, то есть какая то шестёрка уже точно найдётся. Следовательно, если уже какая то шестёрка есть, значит нам необходимо и достаточно взять 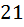монет, чтобы среди них нашлось 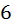монет одного достоинство.

Ответ: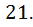

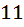Задача: Есть пуговица одного из цветов. Докажите, что либо найдется 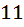пуговиц одного цвета, либо найдётся 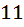пуговиц все цвета которых разные.

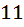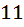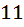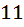Решение: Давайте действуем методом от противного. Предположим неверно ни первое утверждение, ни второе утверждение, то есть предположим, что нет пуговиц одного цвета, и нет пуговиц разного цвета. Давайте прежде всего привяжемся ко второму предположению. То есть что значит, что нет пуговиц разного цвета? –Это в на самом деле означает, что среди наших пуговиц все цветов не задействованы. Следовательно из этой предположений выходит, что задействованы не более чем 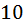цветов. Теперь давайте посмотрим на первое предположение, то есть, нет 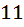пуговиц одного цвета. Это означает, что пуговиц каждого конкретного цвета не больше 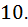И используя выводы которые мы нашли в наших двух предположениях следуем так: Задействовано не больше чем 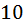цветов, т. е, есть(имеем) сколькото пуговиц первого цвета, есть сколькото пуговиц второго цвета, ... , и так далее, ... , номер 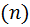последнего цвета не превосходит десяти, то есть сколько то пуговиц какого то цвета и вот

номер 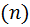этого какого то цвета не превосходит десяти. Ну мы говорим, что есть сколько то пуговиц первого цвета, есть сколько то пуговиц второго цвета, …, сколько то пуговиц последнего цвета номер 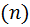которого не превосходит десяти, а мы ещё знаем, что пуговиц каждого цвета не больше десяти. Давайте приведём рисунок и в этом рисунке номера цвета пуговиц–это числа от 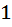до 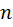. А каждый пуговиц не больше десяти:

1 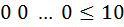( Пуговиц первого цвета, их не больше )

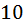2 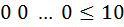( Пуговиц второго цвета, их не больше )

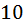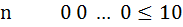( Пуговиц последнего 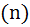цвета, их не больше )

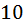И так 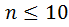( номер последнего цвета ), то получается, что суммарная количество пуговиц в нашем распоряжении 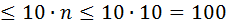, то есть не больше чем 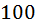–это противоречие, ведь мы знаем, что у нас пуговица. Значит наши предположении были неправильными. ЧТД.

⇐ Предыдущая 123 4 Следующая ⇒