Хелпикс

Главная

Контакты

Случайная статья



Пример 3.8. Пример 3.9. Решение. Пример 3.10. Решение

⇐ ПредыдущаяСтр 5 из 6Следующая ⇒


Пример 3. 8

Решить уравнение .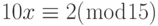

Сначала мы найдем НОД(10, 15) = 5. Полученное число 5 не делится на 2, решение отсутствует.

Пример 3. 9

Решить уравнение .

Решение

Заметим, что НОД (14, 18) = 2. Поскольку 2 делит 12, мы имеем точно два решения, но сначала сократим уравнение:

Оба решения, 6 и 15, удовлетворяют уравнению сравнения, потому что , а также .

Пример 3. 10

Решить уравнение .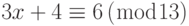

Решение

Сначала мы приводим уравнение к форме 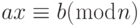. Мы прибавляем (–4) к обеим сторонам ( 4 аддитивная инверсия). Получим 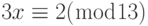. Поскольку НОД (3, 13) = 1, уравнение имеет только одно решение, 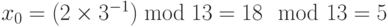. Мы можем видеть, что ответ удовлетворяет первоначальному уравнению: .

Система линейных уравнений, содержащих сравнения

Мы можем решить систему линейных уравнений с одним и тем же модулем, если матрица, сформированная из коэффициентов системы уравнений, имеет обратную матрицу. Для решения уравнения составляются три матрицы. Первая — квадратная матрица — формируется из коэффициентов уравнения. Вторая — матрица-столбец — составляется из переменных. Третья — матрица-столбец в правой стороне оператора сравнения — состоит из значения bn. Мы можем это уравнение представить как произведение матриц. Если обе стороны сравнения умножить на мультипликативную инверсию первой матрицы, в результате мы получим решение системы уравнений, как это показано на рис. 3. 9.


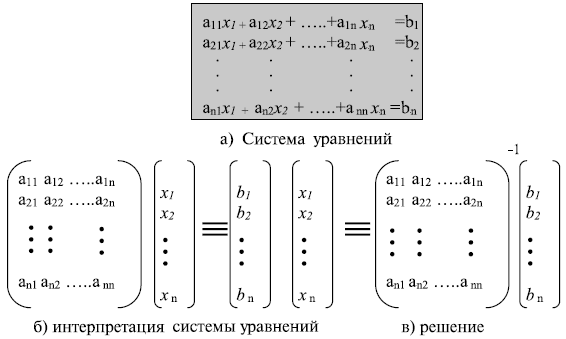
Рис. 3. 9. Система линейных уравнений


⇐ Предыдущая123456Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.