Пример 3.7. Сравнение

Пример 3. 7

Рисунок 3. 8 показывает матрицу вычетов в Z_n и его мультипликативной инверсииA^-1. Возьмем детерминантdet (A) = 21, который имеет мультипликативную инверсию5 в Z₂₆. Обратите внимание, что когда мы умножаем эти две матрицы, то результат — единичная матрица мультипликативная матрица, в Z₂₆.

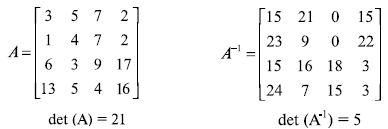
Рис. 3. 8. Матрица вычетов и мультипликативная инверсия

Сравнение

Две матрицы, сравнимые по модулю n, записываются как 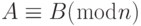, если они имеют одинаковое число строк и столбцов и все соответствующие элементы — сравнимые по модулю n. Другими словами, 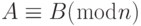, если 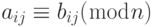для всех i и j.

3. 2. Линейное уравнение

Криптография часто включает в себя решение уравнения или множества уравнений одной или более переменных с коэффициентом в Z_n. Этот раздел показывает, как решать уравнения с одним неизвестным, когда степень переменной равна 1 (линейное уравнение).

Линейные уравнения с одним неизвестным, содержащие сравнения

Давайте посмотрим, как решаются уравнения с одним неизвестным, содержащие сравнения, то есть уравнения ax = b (mod n). Уравнение этого типа может не иметь ни одного решения или иметь ограниченное число решений. Предположим, что НОД (a, n) = d. Если d†b, решение не существует. Если d|b, то имеется d решений.

Если d|b, то для того, чтобы найти решения, мы используем следующую стратегию.

1. Сократить уравнение, разделив обе стороны уравнения (включая модуль) на d.

2. Умножить обе стороны сокращенного уравнения на мультипликативную инверсию, чтобы найти конкретное решение x₀.

3. Общие решения будут x = x₀ + k (n/d) для k = 0, 1..., (d – 1).

⇐ Предыдущая 1 2 345 6 Следующая ⇒