Пример 3.2. Пример 3.3. Пример 3.4. Детерминант. Пример 3.5. Пример 3.6

Пример 3. 2

Рисунок 3. 3 показывает произведение матрицы-строки ( ) на матрицу-столбец ( ). В результате получаем матрицу размером .

Рис. 3. 3. Умножение матрицы-строки на матрицу-столбец

Пример 3. 3

Рисунок 3. 4 показывает произведение матрицы на матрицу . В результате получаем матрицу

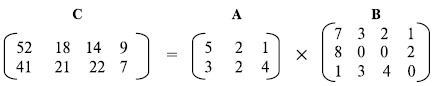
Рис. 3. 4. Умножение матрицы 2 x 3 на матрицу 3 x 4.

Скалярное умножение

Мы можем также умножить матрицу на число (называемое скаляр ). Если A — матрица 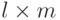и x — скаляр, то C = xA — матрица 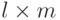, в которой .

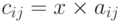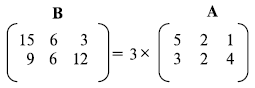
Рис. 3. 5. Скалярное умножение

Пример 3. 4

Рисунок 3. 5 показывает пример скалярного умножения.

Детерминант

Детерминант — квадратная матрица A размера 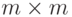, обозначаемая как det (A) — скалярное вычисление рекурсивно, как это показано ниже:

где A_ij получается из A удалением i -той строки j -того столбца.

Детерминант определяется только для квадратной матрицы.

Пример 3. 5

Рисунок 3. 6 показывает, как можно вычислить детерминант матрицы , базируясь на детерминанте матрицы и используя приведенное выше рекурсивное определение. Пример доказывает, что когда m1 или 2, это позволяет найти детерминант матрицы достаточно просто.

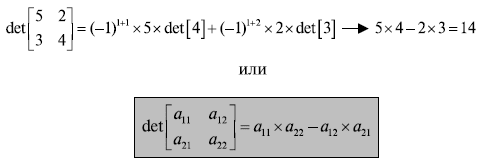
Рис. 3. 6. Вычисление детерминанта матрицы 2 x 2

Пример 3. 6

Рисунок 3. 7 показывает вычисление детерминанта матрицы .

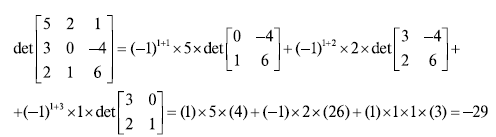
Рис. 3. 7. Вычисление детераминаната матрицы 3 x 3

⇐ Предыдущая 123 4 5 6 Следующая ⇒