Контакты

Случайная статья

2 ø è

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Задание 1

Исходные данные:

Даны точки

A(2, 1),

B(- 6, -2),

C(- 3, -1).

Решение:

а) p = AB + BC + AC . При вычислении длин сторон можно

воспользоваться формулами из предыдущей практической, учитывая, что

третья координата равна нулю, тогда p = AB + BC + AC

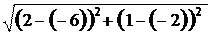
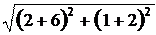
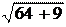
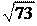AB = = = = ,

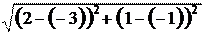
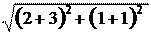AC = =

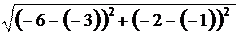BC = =

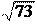
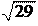
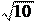p = + + .

= = ,

= =

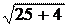
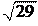
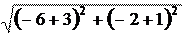
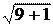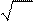10,

б) уравнение AB :

x - 2 =

y -1

Þ x - 2 = y -1 Þ 3(x - 2) = 8(y -1)Þ 3x - 8y + 2 = 0

- 6 - 2

- 2 -1

- 8 - 3

уравнение AC :

x - 2 =

y -1 Þ

x - 2 = y -1 Þ 2(x - 2) = 5(y -1)Þ 2x - 5y +1 = 0

- 3 - 2

-1-1

- 5 - 2

уравнение BC :

x + 3 =

y +1 Þ

x + 3 = y +1 Þ x + 3 = 3(y +1)Þ x - 3y = 0;

- 6 + 3

- 2 +1

- 3 -1

в) координаты середины отрезка ВС: x

= - 6 - 3 = - 9, y

- 2 -1 3

= = -,

^M 2 2 ^M 2 2

тогда уравнение АМ:

x - 2 = y -1

Þ x - 2 = y -1 Þ

x - 2 = y -1;

- 9 - 2

- 3 -1

2

- 13 - 5

2 2

13 5

г) для высоты АН вектор BC = {3, 1} будет вектором нормали, тогда

3× (x - 2)+1× (y -1) = 0, 3x - 6 + y -1 = 0, 3x + y - 7 = 0;

д) в этом случае вектор

BC = {3, 1}

будет направляющим вектором для

искомой прямой:

x - 2 =

3

y -1.

1

Задание 2

Исходные данные:

Даны точки

A(2, 1),

B(- 6, -2)

Решение:

Центр окружности – середина отрезка АВ:

xM 0

= 2 - 6 = -2,

2

y = 1 - 2 = - 1, R =

73 тогда уравнение окружности:

M 0 2

æ

2 2

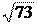1 ö 2 æ ö ²

æ 1 ö 2 73

(x + 2)2 + ç y +

è

÷ = ç

ø è

÷ , (x + 2)2 + ç y +

2 ø è

÷ =.

ø

Задание 3

Исходные данные:

Дана точка

A(2, -3)

Решение:

а) Уравнение параболы, симметричной относительно оси абсцисс:

y² = 2 px ,

находим параметр p (- 3)2

= 2 × p × 2,

4 p = 9,

4 p = 9

p =.

4

Искомое уравнение:

y² = 2 × 9 x

4

y² = 9 x .

2

x2

б) Уравнение параболы, симметричной относительно оси ординат:

y = 2 р ,

находим параметр p

- 3 = 4,

2 р

x2

2 p = - 4, .

3

3x²

Искомое уравнение:

⇐ Предыдущая 1 234 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.