
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Комментарий.. 1. Задание 18 № 507235. Решение.
Комментарий.
Изложим идею решения иными словами.
Обозначим в исходном уравнении 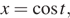
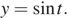 Далее заметим, что при условии
Далее заметим, что при условии 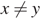 можно избавиться от знаменателя, привести подобные члены и записать исходное уравнение в виде
можно избавиться от знаменателя, привести подобные члены и записать исходное уравнение в виде 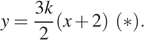 Отметим далее, что в силу введённых обозначений
Отметим далее, что в силу введённых обозначений  Поэтому искомыми являются те значения параметра, при которых прямые, задаваемые уравнением (*), имеют с единичной окружностью (**) точки пересечения, лежащие в первой координатной четверти (
Поэтому искомыми являются те значения параметра, при которых прямые, задаваемые уравнением (*), имеют с единичной окружностью (**) точки пересечения, лежащие в первой координатной четверти ( 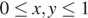 ) и отличные от точек прямой
) и отличные от точек прямой 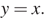
Ответ: 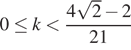 или
или 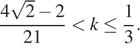
1. Задание 18 № 507235
Найдите все значения параметра а, при каждом из которых множество решений неравенства
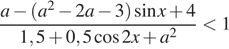
содержит отрезок 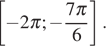
Решение.
Заметим, что при любых значениях переменной 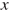 и параметра
и параметра 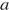 знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству
знаменатель дроби в левой части неравенства положителен, поэтому исходное неравенство равносильно неравенству 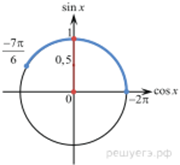
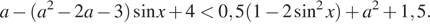
Для того, чтобы множество решений неравенства содержало отрезок  синус должен принимать все значения
синус должен принимать все значения 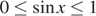 (см. рисунок)
(см. рисунок)
Пусть 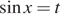 , тогда неравенство принимает вид
, тогда неравенство принимает вид

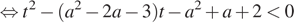
Рассмотрим функцию 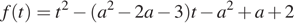 Для того, чтобы множество решений последнего неравенства содержало отрезок
Для того, чтобы множество решений последнего неравенства содержало отрезок 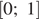 необходимо и достаточно, чтобы одновременно выполнялись два условия
необходимо и достаточно, чтобы одновременно выполнялись два условия 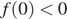 и
и 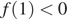


Ответ: 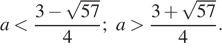
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|