1. Задание 18 № 507224. Решение.. 2. Задание 18 № 515710. Решение.

1. Задание 18 № 507224

Найдите все значения параметра k, при каждом из которых уравнение 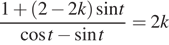имеет хотя бы одно решение на интервале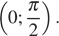

Решение.

Обозначим в исходном уравнении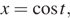

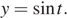
Имеем:

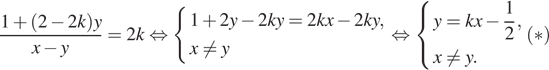
Отметим далее, что в силу введённых обозначений Поэтому искомыми являются те значения параметра, при которых прямые, задаваемые уравнением , имеют с единичной окружностью точки пересечения, лежащие в первой координатной четверти ( 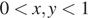) и отличные от точек прямой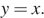

В системе координат, изображённой на рисунке, уравнение задаёт пучок прямых (отмечены красным цветом), проходящих через точку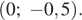

Найдем угловой коэффициент прямой, проходящей через (1; 0): 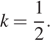У прямой, проходящей через точку 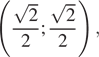угловой коэффициент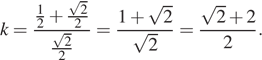

Таким образом, условие задачи выполняется, если

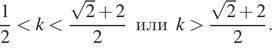
Ответ: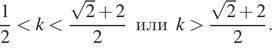

2. Задание 18 № 515710

Найдите все значения k, при каждом из которых уравнение

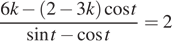
имеет хотя бы одно решение на отрезке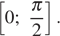

Решение.

ОДЗ данного уравнения: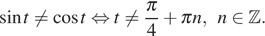

Задачу можно переформулировать так: найдите все значения k, при каждом из которых уравнение

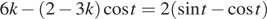
имеет на отрезке 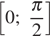хотя бы одно решение, не равное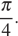

Преобразуем уравнение:

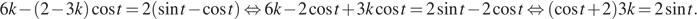
Функция в левой части уравнения на отрезке 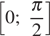монотонно убывает от 9k до 6k. Функция в правой части монотонно возрастает от 0 до 2. Таким образом, уравнение на отрезке 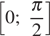будет иметь единственный корень в случае если и то есть при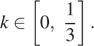

Осталось только выкинуть случай, когда единственный корень попадает в точку 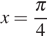. В этом случае получим:

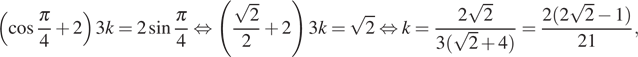
откуда получаем ответ.

12 3 4 Следующая ⇒