2. Теоремы о делимости

Теорема 1. Если числа а и b делятся на m, то их сумма и разность делятся на m.

Доказательство: Так как а и b делятся на m, то а=km и b=lm, где k и l –целые числа. Поэтому, а + b=km+lm=(k+l)m и а - b=km-lm=(k-l)m. Так как k+l и k-l – целые числа, то, по определению, а + b и а – b делятся на m.

Теорема справедлива для суммы трех, четырех и более слагаемых.

Следствие 1. Если сумма нескольких слагаемых делится на m и известно, что все эти слагаемые, кроме одного, делятся на m, то и оставшееся слагаемое делится на m.

Доказательство: Пусть s=a₁ + a₂ + … +a_n, где 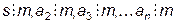, т. е. s=km, a₂=k₂m, a₃=k₃m, …, a_n=k_nm. Докажем, что 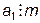. Действительно, а₁= s –( a₂ + … +a_n )= km-k₂m-k₃m-…-k_nm) = m (k-k₂-k₃-…-k_n). Так как k-k₂-k₃-…-k_n – целое число, то .

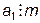Теорема 2. Если a делится на m, b делится на n, то ab делится на mn.

Доказательство: Так как a делится на m и b делится на n, то a=km, b=ln. Тогда ab=(km)× (ln)=(kl)mn, т. е. ab делится на mn.

Заметим, что теорема справедлива и для большего числа множителей.

Следствие 2. Если а делится на m, то aⁿ делится на mⁿ, где n-натуральное число.

Следствие 3. Если хотя бы один из множителей в произведении делится на m, то и само произведение делится на m.

Доказательство: Пусть а делится на m. Так как b-целое число, то b делится на 1. Тогда по теореме 2 ab делится m× 1, т. е. ab делится на m.

(Докажите это следствие иначе, используя определение делимости. )

Пример 1. Дробь 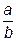сократима. Докажите, что дробь тоже сократима.

Доказательство: Так как дробь 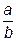сократима, то ее числитель и знаменатель делится на одно и то же целое число. Тогда сумма числителя и знаменателя и их разность тоже делятся на это число (теорема 1). Значит, дробь сократима.

Иначе: так как по условию a=km, b=lm, то a+b=km+lm=(k+l)m, a-b=km-lm=(k-l)m. Тогда 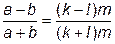, т. е. дробь сократима на m.

Пример 2. Докажите, что если ab+cd делится на a-c, то ad+bc тоже делится на a-c (a¹ c).

Решение: Рассмотрим разность ab+cd и ad+bc. (ab+cd)-(ad+bc)=(ab-bc)-(ad-cd)=(a-c)b-(a-c)d=(a-c)(b-d), т. е. делится на а-с. Но по условию ab+cd делится на a-c. Значит, по следствию 1 ad+bc тоже делится на a-c.

Пример 3. Докажите, что разность любого трехзначного числа и трехзначного числа, записанного теми же цифрами, но в обратном порядке, делится на 9.

Решение: Пусть в трехзначном числе а – цифра сотен, b- цифра десятков и с- цифра единиц. Запишем это число: abc=100а+10b+c. Тогда трехзначное число, записанное теми же цифрами в обратном порядке: cba=100с+10b+а. Их разность abc-cba=100а+10b+c-100с--10b-а=99a-99c=9× 11× (a-c), т. е. делится на 9.

⇐ Предыдущая 123 4 Следующая ⇒