
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача №2.. Пусть производится 8 независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 0,7. Найти вероятность того, что в 8 испытаниях событие А. появится 4 раза.. Задача №3.. Случайная дискретная величина задана ряд
Задача №2.
Пусть производится 8 независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна 0,7. Найти вероятность того, что в 8 испытаниях событие А. появится 4 раза.
Решение:
Производится 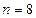 независимых испытаний.
независимых испытаний. 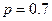 - вероятность появления события А в одном испытании.
- вероятность появления события А в одном испытании.
Событие С – в 8 испытаниях событие А появится 4 раза.
Вероятность события С найдем, используя формулу Бернулли: 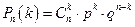 .
.
Вероятность события С равна:
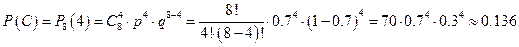 .
.
Ответ: .
Задача №3.
Случайная дискретная величина задана рядом распределения. Найти функцию распределения и построить ее график. Найти математическое ожидание , дисперсию , среднее квадратичное отклонение .
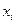
| -1 | |||
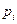
| 0,3 | 0,2 | 0,1 | 0,4 |
Решение:
Найдем функцию распределения 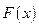 .
.
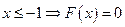 .
.
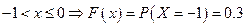 .
.
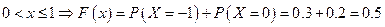 .
.
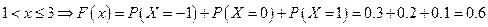 .
.
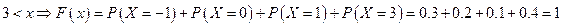 .
.
Функция распределения 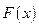 имеет вид:
имеет вид:
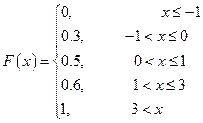
Построим график 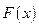 :
:

Найти математическое ожидание:
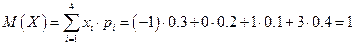 .
.
Найдем дисперсию:
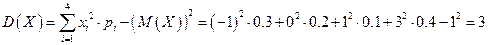 .
.
Найдем среднее квадратическое отклонение:
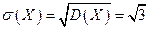 .
.
Задача №4.
Задана непрерывная случайная величина X своей плотностью распределения вероятностей . Требуется: 1) определить коэффициент c; 2) найти функцию распределения ; 3) схематично построить график функций и ; 4) вычислить математическое ожидание и дисперсию X; 5) определить вероятность того, что X примет значение из интервала .
.
Решение:
Определим коэффициент 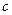 .
.
По свойству плотности распределения вероятностей непрерывной случайной величины: 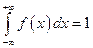 . Тогда:
. Тогда:
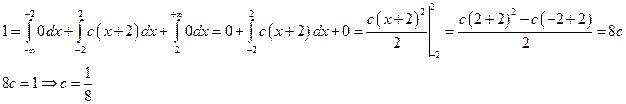 .
.
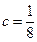 .
.
Плотность распределения имеет вид:
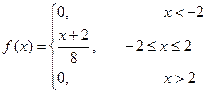
Найдем функцию распределения 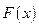 :
: 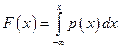
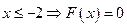 .
.
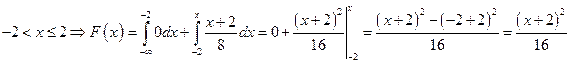 .
.
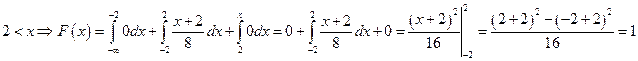 .
.
Функция распределения 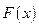 имеет вид:
имеет вид:
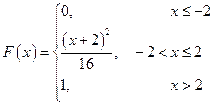 .
.
Построим графики 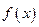 и
и 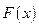 :
:
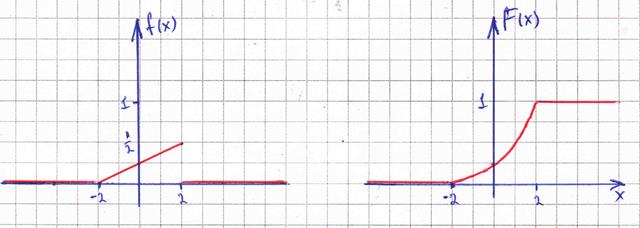
Найдем числовые характеристики.
Математическое ожидание:
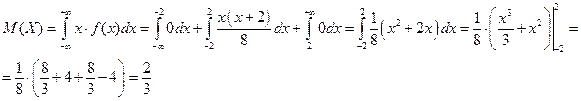 .
.
Дисперсия:
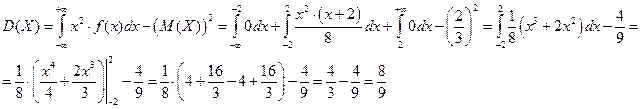
Определим вероятность того, что X примет значение из интервала 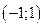 :
:
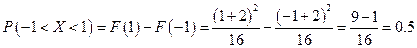 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|