
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача №1.. Из урны, в которой имеется 6 белых и 4 черных шара, извлекаются один за другим три шара. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.
Задача №1.
Из урны, в которой имеется 6 белых и 4 черных шара, извлекаются один за другим три шара. Найти вероятность того, что: а) все три шара будут белыми; б) все три шара будут одного цвета.
Решение:
В урне 10 шаров: 6 белых и 4 черных шара.
Один за другим извлекают три шара.
Событие А – все три вынутых шара белые.
По классическому определению вероятности: 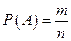 .
.
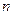 - число всевозможных исходов опыта, т.е. число способов извлечь один за другим три шара: 1-й шар можно вынуть 12 способами, 2-й шар – 11-ю, 3-й – 10-ю, по правилу произведения
- число всевозможных исходов опыта, т.е. число способов извлечь один за другим три шара: 1-й шар можно вынуть 12 способами, 2-й шар – 11-ю, 3-й – 10-ю, по правилу произведения 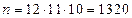 .
.
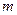 - число благоприятствующих событию А исходов опыта, т.е. число способов извлечь один за другим три белых шара: 1-й белый шар можно вынуть 6 способами, 2-й шар – 5-ю, 3-й – 4-мя, по правилу произведения
- число благоприятствующих событию А исходов опыта, т.е. число способов извлечь один за другим три белых шара: 1-й белый шар можно вынуть 6 способами, 2-й шар – 5-ю, 3-й – 4-мя, по правилу произведения 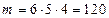 .
.
Вероятность события А равна: 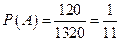 .
.
Событие В – все три вынутых шара одного цвета.
По классическому определению вероятности: 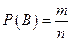 .
.
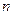 - число всевозможных исходов опыта, т.е. число способов извлечь один за другим три шара: 1-й шар можно вынуть 12 способами, 2-й шар – 11-ю, 3-й – 10-ю, по правилу произведения
- число всевозможных исходов опыта, т.е. число способов извлечь один за другим три шара: 1-й шар можно вынуть 12 способами, 2-й шар – 11-ю, 3-й – 10-ю, по правилу произведения 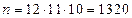 .
.
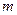 - число благоприятствующих событию В исходов опыта, т.е. число способов извлечь один за другим три белых шара или один за другим три черных шара: 1-й белый шар можно вынуть 6 способами, 2-й шар – 5-ю, 3-й – 4-мя или 1-й черный шар можно вынуть 4-мя способами, 2-й шар – 3-мя, 3-й – 2-мя, по правилу суммы и произведения
- число благоприятствующих событию В исходов опыта, т.е. число способов извлечь один за другим три белых шара или один за другим три черных шара: 1-й белый шар можно вынуть 6 способами, 2-й шар – 5-ю, 3-й – 4-мя или 1-й черный шар можно вынуть 4-мя способами, 2-й шар – 3-мя, 3-й – 2-мя, по правилу суммы и произведения 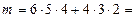 .
.
Вероятность события В равна: 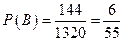 .
.
Ответ: , .
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|