
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант4. Задание 21 № 311618. Решение.. Задание 22 № 338660. Решение.. Задание 23 № 314732. Решение.. Задание 24 № 315053. Решение.. Задание 25 № 341344. Решение.. Задание 26 № 340191. Решение.. алгебра. геометрия
Вариант4
Задание 21 № 311618
Решите уравнение 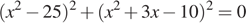 .
.
Решение.
Квадрат любого числа неотрицателен. Сумма двух неотрицательных чисел равна нулю, только если они оба равны нулю. Получаем систему уравнений:
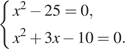
Из первого уравнения  или
или  .
.
Из второго уравнения  или
или  .
.
Системе удовлетворяет единственное значение 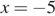 .
.
Ответ: −5.
| Критерии оценивания выполнения задания | Баллы |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Задание 22 № 338660
Первый рабочий за час делает на 10 деталей больше, чем второй, и выполняет заказ, состоящий из 60 деталей, на 3 часа быстрее, чем второй рабочий, выполняющий такой же заказ. Сколько деталей в час делает второй рабочий?
Решение.
Пусть  — число деталей, изготавливаемых первым рабочим за час,
— число деталей, изготавливаемых первым рабочим за час,  , тогда
, тогда 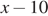 — число деталей, изготавливаемых вторым рабочим за час.
— число деталей, изготавливаемых вторым рабочим за час.
Составим таблицу по данным задачи:
| Производительность (дет/ч) | Время (ч) | Объём работ (дет) | |
| Первый рабочий | 
| 
| |
| Второй рабочий | 
| 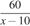
|
Так как первый рабочий справляется с работой на 3 часа быстрее, составим уравнение:
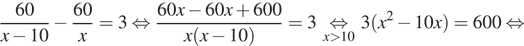
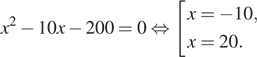
Корень −10 не подходит по условию задачи, следовательно, первый рабочий изготавливает 20 деталей в час. Значит, второй рабочий изготавливает 10 деталей в час.
Ответ: 10.
| Критерии оценивания выполнения задания | Баллы |
| Ход решения задачи верный, получен верный ответ | |
| Ход решения правильный, все его шаги присутствуют, но допущена ошибка или описка вычислительного характера | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 23 № 314732
Известно, что графики функций  и
и 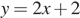 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
Решение.
Найдём абсциссы точек пересечения:
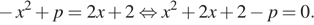
Графики функций, будут иметь ровно одну точку пересечения, если это уравнение имеет ровно одно решение. То есть, если дискриминант этого квадратного уравнения будет равен нулю.

Подставив параметр 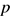 в уравнение, найдём
в уравнение, найдём  координату точки пересечения этих функций:
координату точки пересечения этих функций:
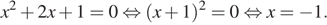
Координата 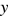 находится путём подстановки координаты
находится путём подстановки координаты  в любое из уравнений, например, во второе:
в любое из уравнений, например, во второе:
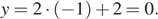
Теперь, зная  можем построить графики обеих функций (см. рисунок).
можем построить графики обеих функций (см. рисунок).
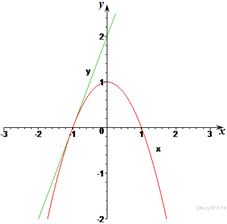
Ответ: (−1; 0).
| Критерии оценивания выполнения задания | Баллы |
График построен правильно, верно указано значение 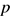 , при которых прямая имеет с параболой только одну общую точку, верно найдены координаты этой точки , при которых прямая имеет с параболой только одну общую точку, верно найдены координаты этой точки
| |
График построен правильно, указаны не все верные значения 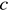
| |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Задание 24 № 315053
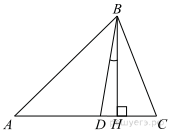
В треугольнике АВС углы А и С равны 40° и 60° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Решение.
Из треугольника 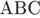 найдем
найдем 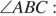
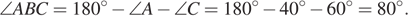
 — биссектриса, следовательно,
— биссектриса, следовательно, 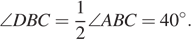
Треугольник 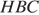 — прямоугольный, следовательно:
— прямоугольный, следовательно:
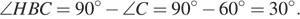
Найдём угол 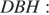
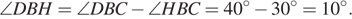
Ответ: 10°.
| Критерии оценивания выполнения задания | Баллы |
| Получен верный обоснованный ответ | |
| При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 25 № 341344
Биссектрисы углов C и D трапеции ABCD пересекаются в точке P, лежащей на стороне AB. Докажите, что точка P равноудалена от прямых BC, CD и AD.
Решение.
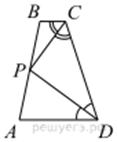 По свойству биссектрисы угла точка P равноудалена от прямых AD и CD (так как лежит на биссектрисе угла D ) и равноудалена от прямых BC и CD (так как лежит на биссектрисе угла C). Значит, точка P равноудалена от всех трёх указанных прямых.
По свойству биссектрисы угла точка P равноудалена от прямых AD и CD (так как лежит на биссектрисе угла D ) и равноудалена от прямых BC и CD (так как лежит на биссектрисе угла C). Значит, точка P равноудалена от всех трёх указанных прямых.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы. | |
| Доказательство в целом верное, но содержит неточности. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Максимальный балл |
Задание 26 № 340191
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 72, тангенс угла BAC равен  Найдите радиус окружности, вписанной в треугольник ABC.
Найдите радиус окружности, вписанной в треугольник ABC.
Решение.
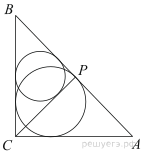
Угол BAC равен углу BCP так как  и
и  . Так как тангенс это отношение противолежащего катета к прилежащему, имеем:
. Так как тангенс это отношение противолежащего катета к прилежащему, имеем: 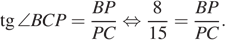 Тогда
Тогда 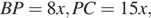 а гипотенуза
а гипотенуза 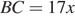 по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на радиус вписанной окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
по теореме Пифагора. Площадь треугольника равна произведению половины его периметра на радиус вписанной окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
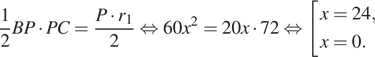
Таким образом, 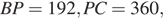 а
а 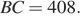 Так как
Так как 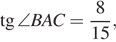 то
то  а
а  по теореме Пифагора.
по теореме Пифагора.
В треугольнике 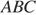 площадь равна произведению половины его периметра на радиус вписанной в него окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:
площадь равна произведению половины его периметра на радиус вписанной в него окружности, но площадь прямоугольного треугольника равна половине произведения катетов, имеем:

Ответ: 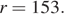
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ. | |
| Ход решения верный, чертёж соответствует условию задачи, но пропущены существенные объяснения или допущена вычислительная ошибка. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Максимальный балл |
Вариант 4
алгебра
| 1,35 | 0,25 | 2,25 |
геометрия
| 22,5 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|