Вариант 2. Задание 21. Решение.. Задание 22 № 353583. Решение.. Задание 23 № 314710. Решение.. Решение.. Решение.. Задание 26 № 351475. Решение.. Вариант2. алгебра. геометрия

Вариант 2

Задание 21

Решите систему уравнений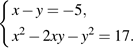

Решение.

Подставим 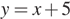во второе уравнение системы, получим уравнение относительно 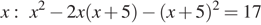. Отсюда и 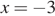. Подставим и 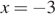в уравнение 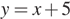, получим: 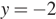и соответственно.

Ответ: (-7; −2), (-3; 2).

Критерии оценивания выполнения задания	Баллы
Правильно выполнены преобразования, получен верный ответ
Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно
Другие случаи, не соответствующие указанным выше критериям
Максимальный балл

Задание 22 № 353583

Первые 2 часа автомобиль ехал со скоростью 65 км/ч, следующие 4 часа — со скоростью 105 км/ч, а последние 4 часа — со скоростью 80 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути.

Решение.

Средняя скорость - это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден.

Найдем длину пути: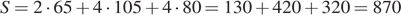

Найдем суммарное время, за которое этот путь был пройден: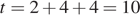

Таким образом, средняя скорость равна:

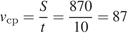км/ч

Ответ: 87

Задание 23 № 314710

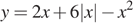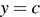Постройте график функции и определите, при каких значениях прямая имеет с графиком ровно три общие точки.

Решение.

Раскрывая модуль, получим, что график функции можно представить следующим образом:

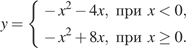
Этот график изображён на рисунке:

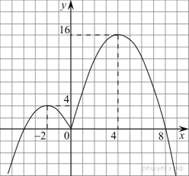
Из графика видно, что прямая 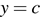имеет с графиком функции ровно три общие точки при и

Ответ: 0; 4.

Задание 24 № 339611Биссектрисы углов A и D параллелограмма ABCD пересекаются в точке, лежащей на стороне BC. Найдите BC, если AB = 34.

Решение.

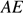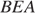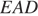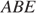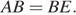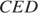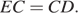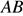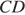По определению параллелограмма — секущая при параллельных прямых, следовательно, углы и равны как накрест лежащие. Поскольку треугольник — равнобедренный, откуда Аналогично, треугольник — равнобедренный и Стороны и равны, как противоположные стороны параллелограмма, следовательно, 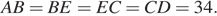Таким образом,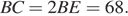

Ответ: 68.

Критерии оценивания выполнения задания	Баллы
Получен верный обоснованный ответ
При верных рассуждениях допущена вычислительная ошибка, возможно приведшая к неверному ответу
Другие случаи, не соответствующие указанным критериям
Максимальный балл

Задание 25 № 316386В окружности через середину O хорды BD проведена хорда AC так, что дуги AB и CD равны. Докажите, что O — середина хорды AC.

Решение.

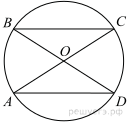
Вписанные углы ADB, CBD , ACB и DAC опираются на равные дуги, значит, они равны.

Получаем, что треугольники СOВ и AOD подобны по двум углам; их коэффициент подобия равен BO:OD. Поскольку BO = OD , эти треугольники равны, следовательно, AO = OC.

Критерии оценивания выполнения задания	Баллы
Доказательство верное, все шаги обоснованы
Доказательство в целом верное, но содержит неточности
Другие случаи, не соответствующие указанным критериям
Максимальный балл

Задание 26 № 351475

Углы при одном из оснований трапеции равны 86° и 4°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 4 и 1. Найдите основания трапеции.

Решение.

Пусть ABCD — данная трапеция, AD — большее основание, K и L — середины сторон AB и CD соответственно. Сумма углов при одном из оснований равна (86° + 4°) = 90°, так что это большее основание AD. Продлим боковые стороны трапеции до пересечения в точке O (см. рис.). Легко видеть, что ∠AOD = 180° − (86° + 4°) = 90°.

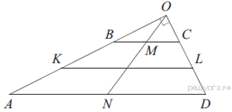
Пусть N — середина основания AD. Тогда ON = — медиана прямоугольного треугольника AOD. Поскольку медиана ON делит пополам любой отрезок с концами на сторонах AO и DO треугольника AOD и параллельный стороне AD, она пересекает основание BC также в его середине M.

Значит, 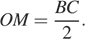Таким образом, Средняя линия KL при этом равна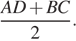

Получаем, что

Ответ: 5; 3.

Критерии оценивания выполнения задания	Баллы
Ход решения задачи верный, получен верный ответ.
Ход решения правильный, все его шаги присутствуют, но допущена ошибка или описка вычислительного характера.
Другие случаи, не соответствующие указанным критериям.
Максимальный балл

Вариант2

алгебра


		3,36			3,75			-27	0,7			1,5	2,25

геометрия


	0,1		1,5

⇐ Предыдущая 123 4 Следующая ⇒