
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант1. Задание 21 № 338566. Решение.. Задание 22 № 314536. Решение.. Задание 23 № 352545. Решение.. Задание 24 № 340968. Решение.. Задание 25 № 355303. Решение.. Задание 26 № 333132. Решение.. алгебра. геометрия
Вариант1
Задание 21 № 338566
Решите неравенство 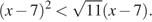
Решение.
Преобразуем неравенство:
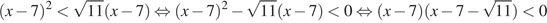
Произведение двух множителей меньше нуля тогда и только тогда, когда множители имеют разный знак, поэтому:
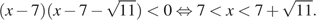
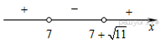
Ответ: 
| Критерии оценивания выполнения задания | Баллы |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Задание 22 № 314536
Туристы проплыли на лодке от лагеря некоторое расстояние вверх по течению реки, затем причалили к берегу и, погуляв 3 часа, вернулись обратно через 5 часов от начала путешествия. На какое расстояние от лагеря они отплыли, если скорость течения реки равна 3 км/ч, а собственная скорость лодки 9 км/ч?
Решение.
Пусть S км — расстояние, на которое от лагеря отплыли туристы. Зная, что скорость течения реки — 3 км/ч, а скорость лодки — 9 км/ч, найдём, что время, за которое они проплыли туда и обратно, составляет 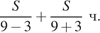 Учитывая, что они были на стоянке 3 часа и вернулись через 5 часов после отплытия можно составить уравнение:
Учитывая, что они были на стоянке 3 часа и вернулись через 5 часов после отплытия можно составить уравнение:
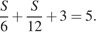
Отсюда S = 8 км.
Ответ: 8 км.
| Критерии оценивания выполнения задания | Баллы |
| Правильно составлено уравнение, получен верный ответ | |
| Правильно составлено уравнение, но при его решении допущена вычислительная ошибка, с её учётом решение доведено до ответа | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 23 № 352545
Постройте график функции 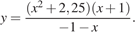 Определите, при каких значениях kпрямая y = kx имеет с графиком ровно одну общую точку.
Определите, при каких значениях kпрямая y = kx имеет с графиком ровно одну общую точку.
Решение.
Преобразуем выражение: 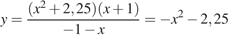 при условии, что
при условии, что 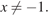
Построим график:

Прямая y = kx имеет с графиком ровно одну общую точку, если она проходит через точку (−1; −3,25) или если уравнение 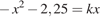 имеет один корень. Дискриминант уравнения
имеет один корень. Дискриминант уравнения 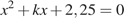 равен
равен 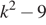 , и он должен быть равен нулю. Получаем, что k = 3,25, k = −3 и k= 3.
, и он должен быть равен нулю. Получаем, что k = 3,25, k = −3 и k= 3.
Ответ: −3; 3; 3,25.
| Критерии оценивания выполнения задания | Баллы |
| График построен правильно, верно найдены искомые значения параметра. | |
| График построен верно, но искомые значения параметра найдены неверно или не найдены. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Максимальный балл |
Задание 24 № 340968
Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB = 18, DC = 54, AC = 48.
Решение.
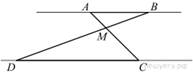 Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные, следовательно, треугольники DMC и BMA подобны по двум углам. Значит,
Углы DCM и BAM равны как накрест лежащие, углы DMC и BMA равны как вертикальные, следовательно, треугольники DMC и BMA подобны по двум углам. Значит,
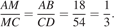
Следовательно,
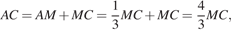 откуда
откуда 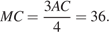
Ответ: 36.
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ. | |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Максимальный балл |
Задание 25 № 355303
Сторона AD параллелограмма ABCD вдвое больше стороны CD. Точка M — середина стороны AD. Докажите, что CM — биссектриса угла BCD.
Решение.
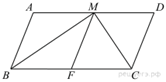
Проведем прямую MF параллельно стороне CD (см. рисунок). Поскольку AM = MD = CD, параллелограмм CDMF является ромбом, поэтому диагональ CM ромба CDMF делит угол FCD пополам. Значит, CM — биссектриса угла BCD.
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Решение не соответствует ни одному из критериев, перечисленных выше | |
| Максимальный балл |
Задание 26 № 333132
Окружности радиусов 14 и 35 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Решение.
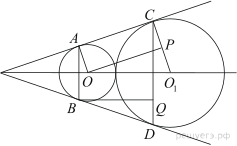
Линия центров касающихся окружностей проходит через их точку касания, поэтому расстояние между центрами окружностей равно сумме их радиусов, т. е. 49. Опустим перпендикуляр OP из центра меньшей окружности на радиус 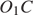 второй окружности. Тогда
второй окружности. Тогда

Из прямоугольного треугольника 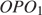 находим, что
находим, что
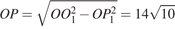
Опустим перпендикуляр 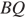 из точки
из точки 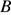 на прямую
на прямую 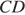 . Прямоугольный
. Прямоугольный
треугольник 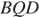 подобен прямоугольному треугольнику
подобен прямоугольному треугольнику 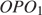 по двум углам, поэтому
по двум углам, поэтому 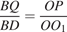 . Следовательно.
. Следовательно.
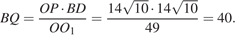
Ответ: 40.
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ. | |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка. | |
| Другие случаи, не соответствующие указанным критериям. | |
| Максимальный балл |
алгебра
| 0,1 | 0,5 | 68,3 |
геометрия
| 0,4 |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|