
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Вариант 3. Задание 21 № 311579. Задание 21 № 311579. Решение.. Задание 22 № 314395. Решение.. Задание 23 № 338207. Решение.. Задание 25 № 340324. Решение.. Задание 24 № 311860. Решение.. Задание 26 № 353380. Решение.. Вариант 3. Алгебра. Геометрия
Вариант 3
Задание 21 № 311579
Упростите выражение: 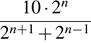 .
.
Задание 21 № 311579
Упростите выражение: 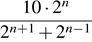 .
.
Решение.
Имеем:
 .
.
Ответ: 4.
| Критерии оценивания выполнения задания | Баллы |
| Правильно выполнены преобразования, получен верный ответ | |
| Решение доведено до конца, но допущена ошибка или описка вычислительного характера, с её учётом дальнейшие шаги выполнены верно | |
| Другие случаи, не соответствующие указанным выше критериям | |
| Максимальный балл |
Задание 22 № 314395
Имеется два сплава с разным содержанием меди: в первом содержится 60%, а во втором — 45% меди. В каком отношении надо взять первый и второй сплавы, чтобы получить из них новый сплав, содержащий 55% меди?
Решение.
Пусть первый сплав взят в количестве x кг, тогда он будет содержать 0,6x кг меди, а второй сплав взят в количестве y кг, тогда он будет содержать 0,45y кг меди. Соединив два этих сплава, получим сплав меди массой x + y, по условию задачи он должен содержать 0,55(x + y) меди. Следовательно, можно составить уравнение:
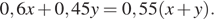
Выразим x через y:
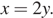
Следовательно, отношение, в котором нужно взять сплавы:
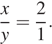
Ответ: 
Задание 23 № 338207
Постройте график функции 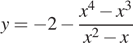 и определите, при каких значениях
и определите, при каких значениях  прямая
прямая  имеет с графиком ровно две общие точки.
имеет с графиком ровно две общие точки.
Решение.
Упростим выражение:
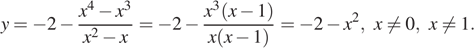
Таким образом, получили, что график нашей функции сводится к графику функции 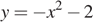 с выколотыми точками
с выколотыми точками  и
и 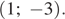 Построим график функции (см. рисунок):
Построим график функции (см. рисунок):
График функции 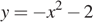 — парабола — получается из графика функции
— парабола — получается из графика функции 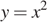 сдвигом на
сдвигом на  и отражением через ось Ox.
и отражением через ось Ox.
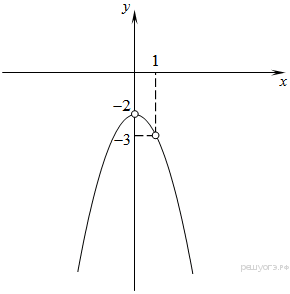
Из графика видно, что прямая 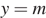 имеет с графиком функции ровно две общие точки при
имеет с графиком функции ровно две общие точки при 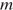 принадлежащем промежутку
принадлежащем промежутку 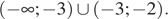
Ответ: 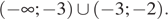
Задание 25 № 340324
Окружности с центрами в точках O1 и O2 не имеют общих точек, и ни одна из них не лежит внутри другой. Внутренняя общая касательная к этим окружностям делит отрезок, соединяющий их центры, в отношении m:n. Докажите, что диаметры этих окружностей относятся как m:n.
Решение.
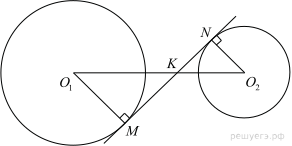 Проведём построения и введём обозначения, как показано на рисунке. Пусть
Проведём построения и введём обозначения, как показано на рисунке. Пусть 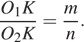 Рассмотрим треугольники
Рассмотрим треугольники 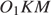 и
и 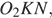 они прямоугольные, углы
они прямоугольные, углы 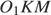 и
и 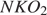 равны как вертикальные, следовательно, треугольники подобны, откуда
равны как вертикальные, следовательно, треугольники подобны, откуда 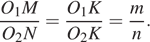
| Критерии оценивания выполнения задания | Баллы |
| Доказательство верное, все шаги обоснованы | |
| Доказательство в целом верное, но содержит неточности | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 24 № 311860
Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.
Решение.
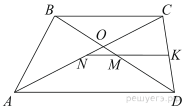
Пусть в трапеции ABCD с основаниями BC = 16 и AD = 34. Обозначим середину диагонали AC через N, середину диагонали BDчерез M, а середину стороны CD через K.
Тогда NK — средняя линия треугольника ACD, MK — средняя линия треугольника BCD. Длина средней линии треугольника равна половине стороны, параллельной ей, то есть MK = BC/2 = 8, NK = AD/2 = 17. Значит, точки N, M и K лежат на одной прямой, и NM = NK− MK = 9.
Ответ: 9.
| Критерии оценивания выполнения задания | Баллы |
| Ход решения верный, все его шаги выполнены правильно, получен верный ответ | |
| Ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна вычислительная ошибка | |
| Другие случаи, не соответствующие указанным критериям | |
| Максимальный балл |
Задание 26 № 353380
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 84. Найдите стороны треугольника ABC.
Решение.
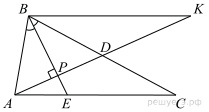 Пусть
Пусть  — точка пересечения отрезков
— точка пересечения отрезков 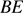 и
и 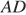 (см. рис.). Треугольник
(см. рис.). Треугольник 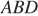 — равнобедренный, так как его биссектриса
— равнобедренный, так как его биссектриса  является высотой. Поэтому
является высотой. Поэтому
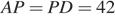 ;
; 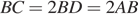 .
.
По свойству биссектрисы треугольника
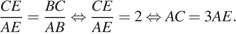
Проведём через вершину  прямую, параллельную
прямую, параллельную  . Пусть
. Пусть 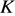 — точка пересечения этой прямой с продолжением медианы
— точка пересечения этой прямой с продолжением медианы 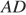 . Тогда
. Тогда 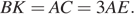
Из подобия треугольников 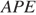 и
и 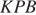 следует, что
следует, что 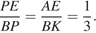 Поэтому
Поэтому 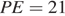 и
и  Следовательно
Следовательно
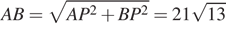 ;
; 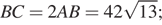
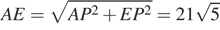 ;
; 
Ответ: 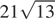 ;
; 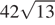 ;
; 
Вариант 3
Алгебра
| 0,8 | -0,20,2 | 0,2 | 1,7 |
Геометрия
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|