Хелпикс

Главная

Контакты

Случайная статья



Математика

⇐ ПредыдущаяСтр 4 из 4


@@@ Математика

 

$$$  анықтауышының мәні:

# +

# +

# -

#-

#-

#+

 

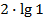
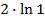
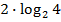
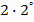
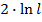
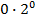
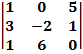$$$ анықтауышының мәні:

#-

# +

#-

#-

#-

# +

#+

 

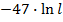
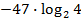
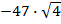
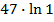
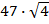
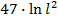
$$$ Векторлық көбейтіндінің қасиеті:

# +

# -

#+

#-

#-

#-

#-

 

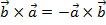
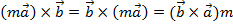
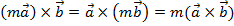
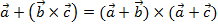
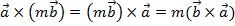
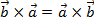
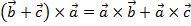
$$$ Векторлардың компланарлық шарты:

#- осы векторлардан құрылған пирамиданың көлемі 1-ге тең

#- осы векторлардан құрылған параллелепипедтің көлемі кез келген оң санға тең

#- аралас туынды теріс санға тең

#+ осы векторлардан құрылған пирамиданың көлемі нөлге тең

#+ осы векторлардан құрылған параллелепипедтің көлемі нөлге тең

 

$$$ Жазықтықтағы кесіндіні берілген λ қатынаста бөлетін нүктенің координатасы:

#+

#-

#-

#-

#-

#-

 

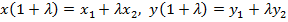
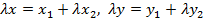
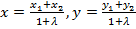
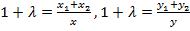
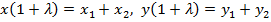
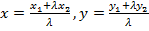
$$$ 3x+2y+7 = 0 және 3x+2y-9 = 0 түзулері:

#- перпендикуляр

#- 30° бұрыш жасайды

#+ бірдей бұрыштық коэффициентке ие

#- 45° бұрыш жасайды

#- әртүрлі бұрыштық коэффициентке ие

# + 0° бұрыш жасайды

# + параллель

 

$$$ Жинақтылықтың қажетті шарты орындалатын қатар:

# -

# +

#-

#+

#-

#+

 

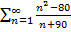
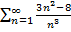
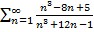
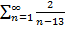
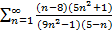
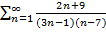
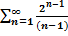$$$ қатарының бесінші мүшесі:

# -

#-

#-

# +

#+

#+

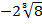
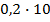
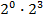
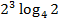
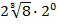
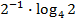
#- g w:val="KZ"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">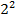

 

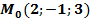$$$  нүктесінен 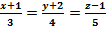түзуіне дейінгі арақашықтық:

# -

#-

# +

#-

#+

# +

 

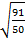
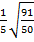
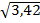
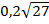
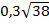
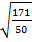
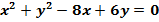$$$ шеңберінің радиусы жататын аралық:

# -[10;12]

#- [9;11]

#- [6;8]

#- [8;10]

#+ [5;7]

#+ [4;6]

#+ [3;5]

 

$$$ Үлкен жарты ось 5-ке және кіші жарты ось 3-ке тең болатын эллипстің теңдеуі:

# +

#-

#+

#-

#+

 

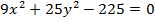
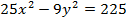
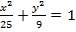
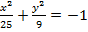
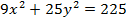
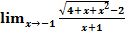$$$ шегі:

#- -1-ден кіші

# +0-ден кіші

#- 0-ге тең

#- - 0,25-тен үлкен

#- 0-ден үлкен

 

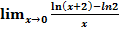$$$ шегі:

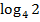
# +1-ден кіші

#+

#-  – кіші

#- 1-ден үлкен

#-

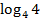
# -  -ден үлкен

# -

 

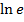
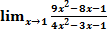$$$ шегінің мәні жататын аралық:

#+ [1;3]

#- [9;10]

#- [5;7]

#- [4;6]

#- [3;5]

# - [6;8]

 

$$$ Радиусы r = 3,02 болатын дөңгелек ауданының жуық мәні:

# +4,56∙2π

#- 3,12∙3π

# +3,04∙3π

#- 4,62∙2π

#- 9,36π

# - 4,68∙2π

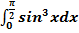$$$ интегралы:

#-

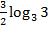
#- g w:val="KZ"/></w:rPr><m:t>-1</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">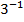

#- -2

#-

# +

#+

 

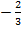
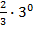
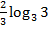
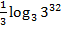
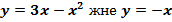$$$ сызықтарымен шектелген фигураның ауданы:

#-

#-

# +

#+

#+

 

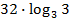
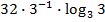
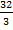
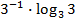
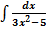$$$ интегралы:

# +

#-

#-

#-

#-

 

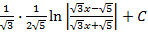
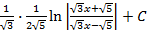
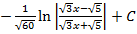
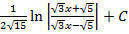
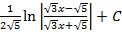
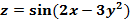$$$  функциясының толық дифференциалы dz = :

# +

# -

#-

#-

#-

#-

# +

 

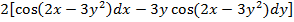
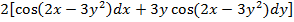
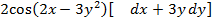
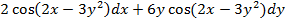
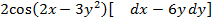
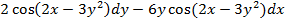
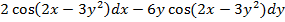
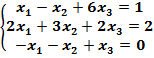$$$ теңдеулер жүйесінің шешімдері мына теңдеуді қанағаттандырады:

#-

#-

# +

#-

# +

#-

#-

 

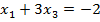
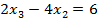
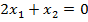
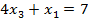
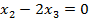
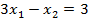
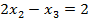
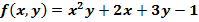$$$ функциясы үшін 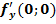нүктесіндегі дербес туындысының мәні:

#- -27

# +

#-

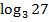
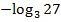
#- 27

#- -3

# + 0,03∙102

 

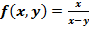$$$ функциясы үшін 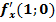нүктесіндегі дербес туындысының мәні мына аралықтарда жатады:

#- (1;3)

# +(-3;3)

#- (2;3)

# +(-1;3)

# +(-1;1)

 

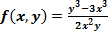$$$ функциясы біртекті болса, онда оның біртектілік дәрежесі:

#-

#-

#-

#-

#-

# +

#+

# +

 

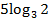
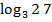
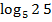
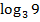
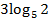
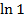
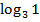
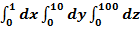$$$ интегралының мәні:

#-

#-

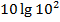
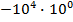
#- ng w:val="KZ"/></w:rPr><m:t>2</m:t></m:r></m:sup></m:sSup></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">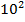

# +

#+

 

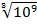
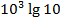
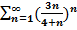$$$ қатары Кошидің радикалдық белгісі бойынша:

#- жинақсыз, өйткені q = 2

# +жинақсыз, өйткені q > 2

#- жинақты, өйткені q = 0

#- жинақты, өйткені q < 2

#- жинақты

#- жинақты, өйткені q = 1/2

 

 

⇐ Предыдущая1234
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.