
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Математика. параметрлік функциясының (1) туындысы;. шегінің мәні жататын аралық;. y = қисығының х1= және х2= аралығындағы ұзындығы;. интегралы;. z = e3x cos2y функциясының д
@@@ Математика
$$$ Мына өлшемді матрицалардың көбейтіндісін табуға болады:
# - А1х3 және В1х2
# + А1х2 және В2х2
# - А2х3 және В2х2
# - А3х1 және В2х2
# + А3х3 және В3х1
# - А3х2 және В4х2
# - А2х3 және В1х2
$$$ 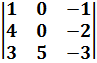 анықтауышының мәні:
анықтауышының мәні:
# - 5· 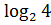
# - 5· 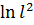
# + -5· 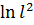
# - 5· 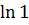
# - 5· 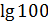
# - -5· 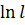
$$$ 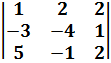 анықтауышының мәні:
анықтауышының мәні:
# + 61· 20
# - 61· 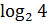
# - 61· 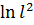
# - 61· 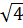
# + 61· 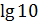
# - 61· 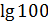
$$$ 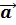 =
= 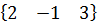 және
және 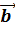 =
= 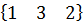 векторларының скалярлық көбейтіндісінің мына аралықта:
векторларының скалярлық көбейтіндісінің мына аралықта:
# - 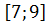
# - 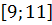
# + 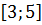
# + 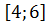
# + 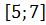
$$$ Векторларға сызықтық амал қолдану кезінде орындалатын қасиет:
# - 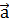 +
+ 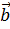
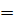 -
- 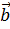 +
+ 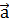
# + α 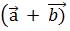 =
= 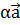 +
+ 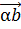
# - -α 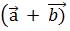 =
= 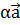 -
- 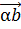
# + 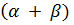 =
= 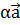 +
+ 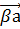 , мұндағы
, мұндағы 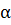 және
және 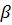 тұрақты
тұрақты
# + 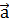 +
+ 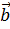
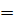
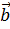 +
+ 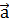
$$$ Ax + By + Cz + 5 = 0 және 2x + 3y + z + 5 = 0 жазықтықтары A, B, C – ның сәйкес параллель мәндері:
# + -2, 3, - 1;
# - 6, - 9, - 3;
# + -6, 9, - 3;
# - - 4, - 6, 2;
# - 2, - 3, -1;
# - - 6, 9, 3;
# + 4, - 6, 2;
$$$ Кеңістіктегі проекциядағы түзу теңдеуі:
# - 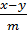 = z;
= z; 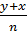 = z;
= z;
# - x – a = yz; y – b = xz
# - x = yz + a; y = xz + b
# - 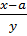 = z;
= z; 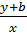 = z;
= z;
# + x – a = mz; y – b = nz
# + x = mz + a; y = nz + b
$$$ Таңбалары айнымалы қатар:
# - 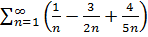
# - 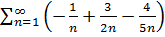
# - 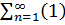 2n
2n 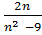
# + 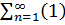 n-1
n-1 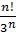
# + 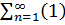 n-1
n-1 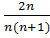
# - 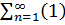 2n
2n 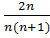
# - 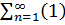 2n
2n 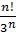
$$$ y = 5x + 7 және y = 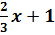 түзулерінің арасындағы бұрыштық аралығы:
түзулерінің арасындағы бұрыштық аралығы:
# + 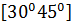
# - 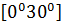
# - 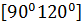
# - 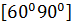
# - 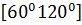
# - 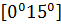
$$$ Нақты осі a = 2 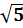 , ал эксцентриситеті ε =
, ал эксцентриситеті ε = 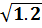 болатын гипербола теңдеуі:
болатын гипербола теңдеуі:
# - x2 – 4y2 = 20
# + 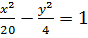
# - x2 – 5y2 + 20=0
# - 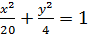
# - 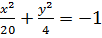
$$$ Фокустарының арақашықтығы 2с 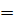 10 , ал төбелерінің арақашықтығы 2а
10 , ал төбелерінің арақашықтығы 2а 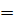 8 болатын гиперболаның теңдеуі:
8 болатын гиперболаның теңдеуі:
# - 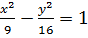
# - 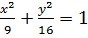
# - 9x2 + 16y2 =144
# - 16x2 – 9y2 - 144=0
# + 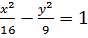
# + 9x2 – 16y2 - 144=0
# + 9x2 - 16y2 =144
$$$ параметрлік функциясының (1) туындысы;
# - 6 – ға тең
# - 4 – ке тең
# + 6 – дан кіші
# - 5 – тен кіші
# - 5 – тен үлкен
# + 4 – тен үлкен
# - 6 – тен үлкен
$$$ шегінің мәні жататын аралық;
# - 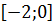
# - 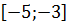
# + 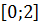
# + 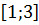
# + 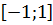
$$$ шегі;
# + 0 – ден үлкен
# - 1 – ге тең
# + 0,5 – ке тең
# - 1 – ден үлкен
# + 1 – ден кіші
# - 0 – ге тең
$$$ y = 2x функциясының n- ші ретті туындысы:
# - y(n) = 2x 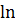 n-12
n-12
# + y(n) = 2x 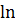 n2
n2
# - y(n) = 2x+1* 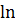 n+12
n+12
# - y(n) = 2x-1 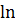 n-12
n-12
# - y(n) = x2x-n 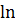 n2
n2
# - y(n) = 2x+1 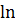 n4
n4
$$$ 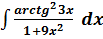 интегралы:
интегралы:
# - 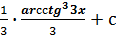
# + 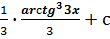
# - 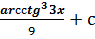
# + 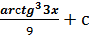
# - - 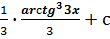
# - - 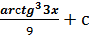
# - 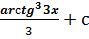
$$$ y = қисығының х1= және х2= аралығындағы ұзындығы;
# - 34◦ ·3-1
# - 3· 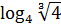
# + 34· 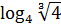
# - 34·3◦
# + 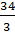
$$$ интегралы;
# - 3· 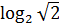
# - 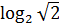
# - 2-1
# + 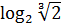
# + 3-1 · 2
# + 
$$$ z = e3x cos2y функциясының дербес туындысы ;
# - 0,6*10-2
# - 0,6*640
# + - 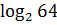
# - 0,6
# - 64
$$$ f(x,y)=x2y+2x+3y – 1 функциясы үшін 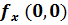 нүктесіндегі дербес туындының мәні;
нүктесіндегі дербес туындының мәні;
# - - 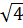
# - 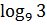
# - -2
# - - 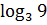
# + 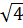
# + 2
# + 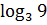
$$$ z= x2 + xy + y2 – 2x функциясының A(- 1 ; 1) нүктесіндегі - нің мәні;
# - - 2 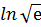
# - - 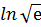
# + 2 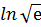
# + 1
# + 2◦
# - 2◦ ·2
# - 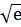
$$$ Екінші ретті сызықтық дифференциалдық теңдеудің y' + 5 y' + 4 y=0 сипаттаушы теңдеуінің түбірлері;
# - k1 =0, k2 = - l
# - k1 =3, k2 = 2
# + k1 = - log2 24 , k2= - log2 2
# + k1 = - 2◦ ·22, k2 = - 2◦
# - k1 = - 2, k2 = 7
# - k1 = 2, k2 = 7
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|