Хелпикс

Главная

Контакты

Случайная статья



теңдеуінің шешімі; 

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


$$$      теңдеуінің шешімі; 

# - x = 3t, y = 21, z = 5t

# + x+y + z = -t

# - x +у + z = 6 t

# +

# -

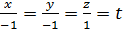
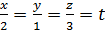
# - x= 2 t, у =t, z = 3t

# -

 

 

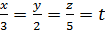
$$$   (3,0) және     ( 0, 2) векторлардан құрылған параллелограммның ауданы;

# - 0 * 31

# - 4 * 30

# - -6 * 30

# - 3 * 30

# + 3 * 21

# + 2 * 31

# - 5 * 30

 

 

$$$   интегралының мәні;

# - log39

# +

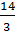
# - 7 * 0,014

# - 0,14 * 10-1

# + 4

# - 0,14 * 10

 

 

$$$ f(x, y)= x2y + 2x+3y – 1 функциясы үшін   (1;0)  дербес туындысы мына аралықтарда жатады;

# - (0; - 1)

# + ( - 1; 3)

# - (-1; 1)

# - ( -1;-2)

# - (-1;-3)

# - (0;1)

 

 

$$$ f(x, y)= x2y + 2x+3y – 1 функциясы үшін   (3;2)  дербес туындысы мына аралықтарда жатады;

# - (2; 3)

# -

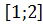
# - ( 1;2)

# + ( 0;5)

# - ( 1;4)

# - ( 1;3)

 

 

$$$ Кеңістіктегі проекциядағы түзу теңдеуі:

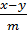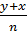# -  = z;  = z;

# -  x – a = yz; y – b = xz

# -  x = yz + a; y = xz + b

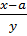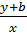# -  = z;  = z;

# + x – a = mz; y – b = nz

# +  x = mz + a; y = nz + b

 

@@@Математика (2016)

1-нұсқа

$$$ А= 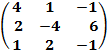, В =  А+В матрицасының мәні:

#-

#-

#-

#-

#+

#+

#+

 

 

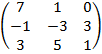
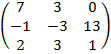
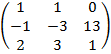
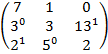
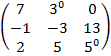
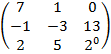
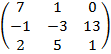
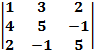$$$  анықтауышының мәні:

#+ -70*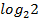

#- 70*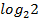

#- 70*ln 1

#-70*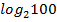

#- 70 *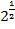

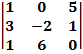$$$  анықтауышының мәні:

#- -47*ln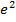

#- 47*ln 1

#+ 47*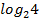

#+ 47*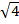

#+ 47*ln e

 

$$$ C= 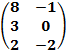, D= 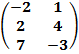, C – 2D матрицасының мәні:

#-

#+

#-

#-

#-

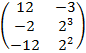
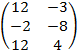
$$$ Анықталған интегралдың негізгі қасиеттері:

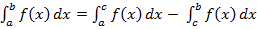#-  мұндағы а ≤ с ≤ b

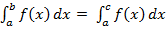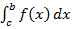#+  +  мұндағы а ≤ с ≤ b

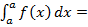#- 1

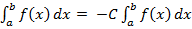#-  мұндағы C тұрақты

#+

#+

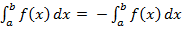
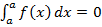
$$$ Айнымалылары ажыратылатын дифференциалдық теңдеу:

#+ x(1+ 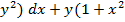)dy = 0

#- xy 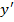=s w:space="720"/></w:sectPr></w:body></w:wordDocument>">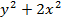

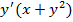#- =y

#- (1+ 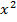)dy – (arctgx - y)dx 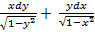= 0

#+  = 0

#+

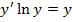
#- x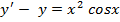

 

$$$ Бірінші ретті дифференциалдық теңдеу:

#-

#-

#-

#+

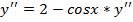
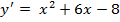
#+ (4+x) =

#+  

 

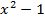
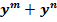$$$ +6

#+ 3*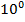

#- 2*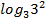

#- 3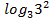

#+ 3 ln e

#- 6 Ln e

#- -3*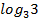

 

$$$ Берілгені: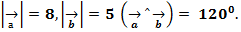

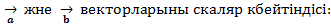
#- -5*lg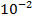

#- 5*ln 1

#- 5*lg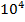

#+ 5*lg

#+ -5*ln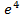

#- -5*lg

#- 5*ln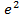

 

$$$  =  =

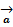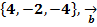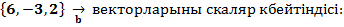
#-11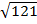

#+ 11*ln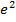

#- 11

#+ 11*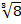

#+ 11*lg100

#- 11* ln e

 

$$$ M(3;-1;-5) нүктесі арқылы өтетін 3x-2y+2z=7=0 және 5x-4y+3z+1=0

Жазықтықтарына перпендикуляр болатын жазықтық теңдеуі:

#- 2x – y + 2z - 15= 0

#- 2x + y - 2z = -15

#+ 2x + y - 2z = 15

#- 2(x – 3) – (y + 1) + 2(z + 5) = 0

#- 2(x + 3) + (y - 1) - 2(z - 5) = 0

#+ 2x + y – 2z – 15 = 0

 

$$$ A(-2;3) және B(1;7) нүктелерінің арақашықтығы келесі аралықта жатыр:

#+ (2;6)

#- (7;11)

#- (8;12)

#- (6;10)

#- (1;5)

#+ (4;8)

#- (5;9)

 

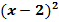$$$ + =25 шеңбердің теңдеуін қанағаттандыратын нүкте:

#- (-2;0)

#+ (5;1)

#- (6;2)

#- (7;3)

#+ (6;0)

#- (5;-1)

#+ (7;-3)

 

$$$  шегінің мәні:

#+

#- *

#+

#-

#+

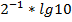
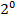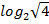
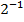
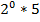
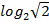
$$$ Егер f(x) =  болса, онда 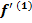 мәні:

#+

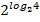
#- 2*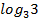

#- 2*lg 10

#- 2*ln e

#- 2*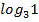

#- 2*lg 1

 

$$$ y = sin x функциясының сегізінші реттегі туындыларының арасында өзара тең болатын туынды:

#+

#- =

#-

#-

#+

#-

 

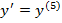
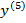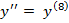
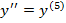
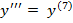
$$$  шектің мәні:

#+ lg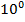

#- ln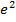

#-

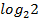
#- lg 10

#- ln e

#- lg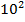

 

$$$

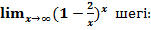
#- e – ге тең

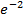#+ -не тең

#- 1-ден үлкен

#- 0- ге тең

#- 1-ге тең

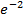#- -нен кіші

 

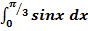$$$  интегралының мәні:

#- 5*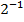

#- 2*

#+ 5*

#-  *

#+

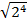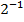
#- 4*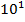

#+

 

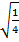
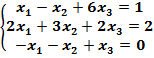$$$  теңдеулер жүйесінің шешімдері мына теңдеуді қанағаттандырады:

#-

#-

#+

#+

#+

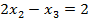
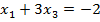
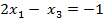
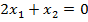
 $$$ y = 2 - 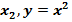 сызықтарымен шектелген фигураның ауданы:

#+ 8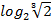

#- 3

#-

#+

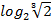
#- 3 *

#- -

#-

$$$ y = 4 - 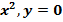 сызықтарымен шектелген фигураның ауданы:

#+

#+

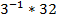
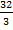
#- ng w:val="EN-US"/></w:rPr><m:t>3</m:t></m:r></m:den></m:f></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">

#-

#-

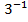
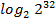
#- 32

$$$ f (x,y) = 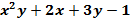 функциясы үшін  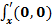нүктесіндегі дербес туындысының мәні:

#+ 2

#+

#-

#-

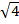
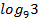
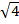
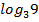
#- -2

#- -

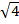
$$$ Z =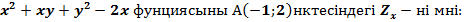

#- -

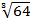
#- 4 lne

#+ -

#+ - *

#-

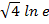
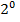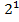
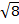
$$$ Екінші ретті сызықтық дифференциалдық теңдеудің 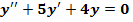сипаттаушы теңдеуінің түбірлері:

#-

#+

#+

#-

#-

 

 

⇐ Предыдущая1234Следующая ⇒
  

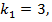
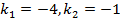
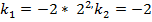
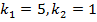
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.