
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Берілгені: 5x2 y - 6x + 2y . z1 x- тің А(1;1) нүктесіндегі мәні;
$$$ Берілгені: 5x2 y - 6x + 2y . z1 x- тің А(1;1) нүктесіндегі мәні;
# - - 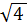 ·2
·2
# + 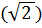 4
4
# - 2◦ ·24
# + 2· 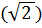 2
2
# - 4 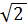
$$$ n2 қатары Кошидің радикалдық белгісі бойынша;
# - жинақсыз, өйткені q = 3
# - жинақты, өйткені q = 0
# - жинақты, өйткені q 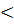 1
1
# + жинақсыз, өйткені q = e
# + жинақсыз
# + жинақсыз, өйткені q 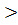 1
1
$$$ қатары Даламбер белгісі бойынша;
# + жинақты, өйткені q 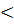 1
1
# - жинақты, өйткені q = 
# - жинақсыз, өйткені q = 2
# + жинақты
# - жинақсыз, өйткені q 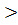 1
1
2-нұсқа
$$$ A =  , B =
, B = 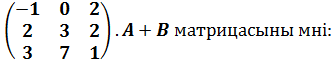
#+ 
#- 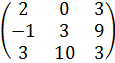
#- 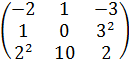
#- 
#- 
$$$ C = 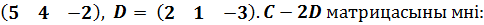
#- ( 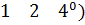
#- 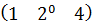
#+ 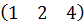
#+ 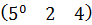
#- 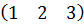
#- 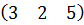
$$$ Мына өлшемдерді матрицалардың айырмасын табуға болады:
#- 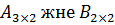
#+ 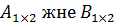
#- 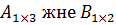
#- 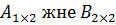
#+ 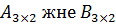
#- 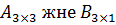
#- 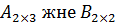
$$$ 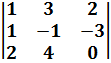 анықтауышының мәні:
анықтауышының мәні:
#+ 3* ln 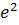
#+ 3* 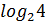
#- -3* ln e
#- -3* ln 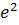
#- -3* 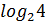
#- 3* ln e
#- -3lg 100
$$$ Анықталмаған интегралдың негізгі қасиеттері:
#+ 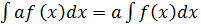 мұндағы
мұндағы 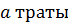
#- d 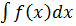 = F (x) + C
= F (x) + C
#+ d 
#+ 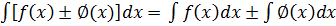
#- 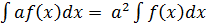 мұндағы
мұндағы 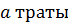
#- 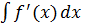 =
= 
$$$ Негізгі интегралдар кестесінің формуласы:
#- 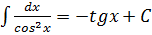
#- 
#- 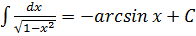
#+ 
#+ 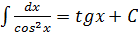
#+ 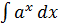 =
= 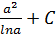
$$$ 5 ( 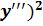 - 3
- 3 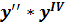 =0 дифференциалдық теңдеуінің реті тең:
=0 дифференциалдық теңдеуінің реті тең:
#- 3 * 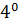
#- 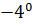
#+ 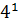
#- -3 * 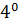
#+ 4 * 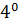
#+ 4 * 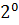
#- 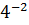
$$$ 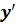 *
* 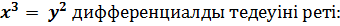
#- 2 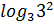
#+ 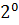
#- -2 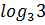
#- 5 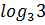
#+ 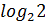
#+ ln e
#- -5 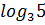
$$$ 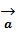 =
= 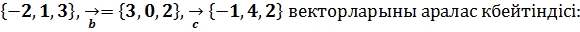
#- - 11 * lg 100
#- - 11 * 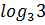
#- 11* ln 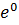
#- - 11 * 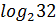
#+ 11* 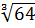
$$$ y = 5x +7 және y = 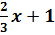 түзулерінің арасындағы бұрыштың аралығы:
түзулерінің арасындағы бұрыштың аралығы:
#- 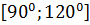
#- 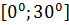
#+ 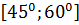
#+ 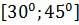
#- 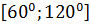
#+ 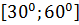
$$$ x-2y + 2z – 8 = 0 және x + z – 6 = 0 жазықтықтарының арасындағы бұрыш:
#- 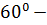 тан үлкен
тан үлкен
#+ 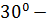 тан үлкен
тан үлкен
#- 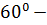 қа тең
қа тең
#+ 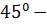 қа тең
қа тең
#- 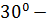 қа тең
қа тең
$$$ 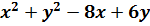 = 0 шеңберінің радиусы жататын аралық:
= 0 шеңберінің радиусы жататын аралық:
#+ 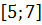
#- 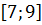
#- 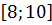
#- 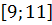
#- 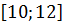
#+ 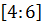
$$$ шегінің мәні;
# - 0.8 * 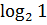
# - 0.8 * 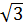
# + 0.8 * lg10
# + 0.8
# - - 0.8 * lg10
# + 0.8 * lne
# - 0.8 * 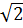
$$$ y = 2x функцясының n –ші ретті туындысы;
# - у(n) = 2x-1 lnn-12
# - у(n) = 2x+1 lnn+12
# + у(n) = 2x (ln2)n
# + у(n) = 2x-1 lnn 4
# + у(n) = 2x lnn 2
$$$ параметрлік функциясының (1) туындысы;
# - 4 – ға тең
# - 6 – дан үлкен
# - 5 – тен кіші
# + 6 – дан кіші
# + 5 – ке тең
$$$ Егер f (x) = 3x – 2 болса, онда мәні;
# + 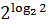
# - 20 * ln e
# - 2 * ln e2
# + 2 * 50
# + 2-1 * 4
$$$ f (x)= функциясының х= 1 нүктесіндегі туындысы;
# + - 0,5 ln e
# - log4 2
# - lg 10
# - 0,5 * lg10
# + log2 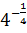
# + - log4 2
# - log2 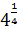
$$$ Сызықтарымен шектелген фигураның ауданы: y = -6x, y=0, x=0, x=4;
# - 34 * 2
# + 23 * ( 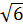 )2
)2
# - 4 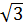
# + 24 * 3
# - (ra)2*34
$$$ y᾿ = sin2x дифференциалдық тендеуінің жалпы шешімі у= :
# +  (sin2 х — cos2 х) + С
(sin2 х — cos2 х) + С
# - ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  cos2 х + С
cos2 х + С
# - -  (sin2 х — cos2 х) + С
(sin2 х — cos2 х) + С
# + - ar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  cos2 х + С
cos2 х + С
# + - 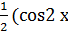 —sin2 х) + С
—sin2 х) + С
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|