
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Произведение непрерывной функции на постоянную величину есть непрерывная функция. Да
3)Произведение непрерывной функции на постоянную величину есть непрерывная функция. Да
4)Если сумма двух данных функций непрерывна, то обе функции непрерывны. Нет
14..Верно ли то, что функция 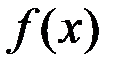 непрерывна везде в своей области определения, если
непрерывна везде в своей области определения, если 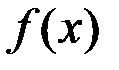 задана соотношением:
задана соотношением:
1) . Да.
2) Да.
3) Нет.
4) Да.
Часть 2. В каждом следующем задании предлагаются несколько утверждений. Необходимо выбрать верное утверждение из предлагаемого набора альтернатив.
15..Пусть задана функция 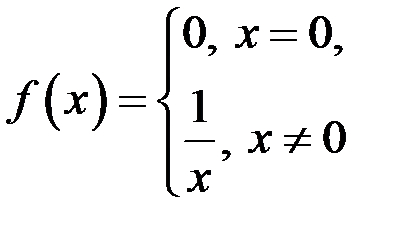 , тогда справедливо утверждение:
, тогда справедливо утверждение:
A)  при
при 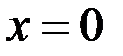 имеет точку разрыва 1 рода.
имеет точку разрыва 1 рода.
Б)  при
при 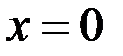 имеет устранимую точку разрыва.
имеет устранимую точку разрыва.
*В)  при
при 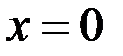 имеет точку разрыва 2 рода.
имеет точку разрыва 2 рода.
Г)  непрерывна при
непрерывна при 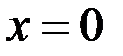 .
.
16..Пусть задана функция
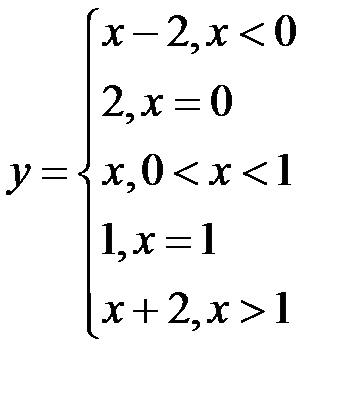
Верны ли утверждения:
А)  и
и 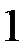 точки разрыва. Да.
точки разрыва. Да.
Б) точка  - точка разрыва первого рода. Да.
- точка разрыва первого рода. Да.
В) точка 1 – точка разрыва второго рода. Нет.
Г) функция непрерывна на всей оси. Нет.
17..Значения параметров 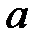 и
и 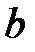 , при которых функция
, при которых функция
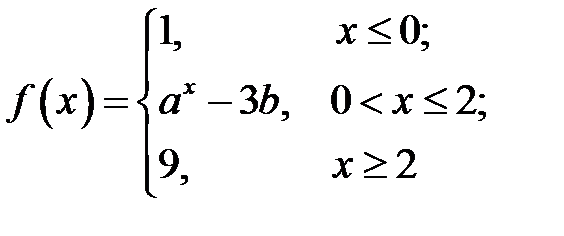
непрерывна на всей оси, равны …
А) 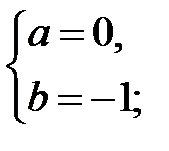
| Б) 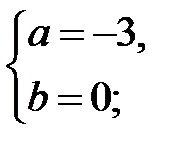
| В) 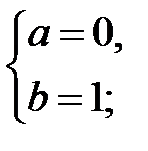
| *Г) 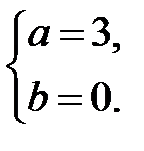
|
18..Значения параметров a и b, при которых функция
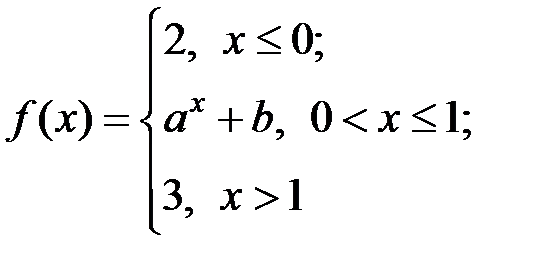 непрерывна на всей числовой оси, равны …
непрерывна на всей числовой оси, равны …
Б) 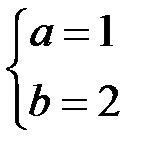
| *А) 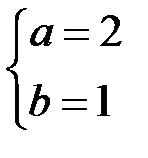
| В) 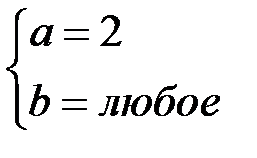
| Г) 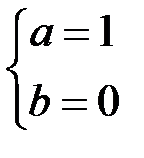
|
19..Значения параметров 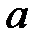 и
и 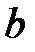 , при которых функция
, при которых функция
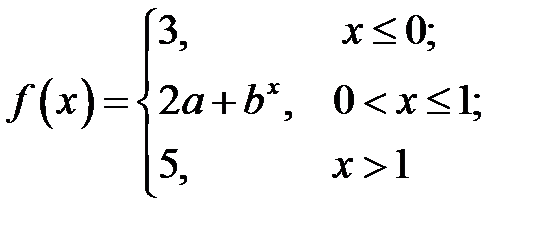
непрерывна на всей оси, равны …
А) 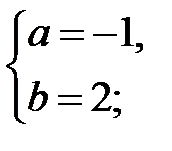
| *Б) 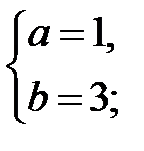
| В) 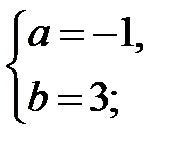
| Г) 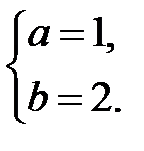
|
20.Функция
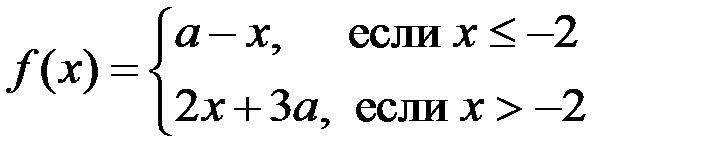
непрерывна в точке 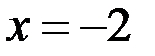 …
…
А) при любом 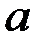
| Б) при 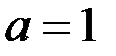
| В) при 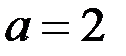
| *Г) при 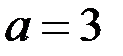
|
21.Дан график функции 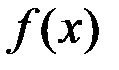
| -1 |
Тогда справедливо утверждение: функция 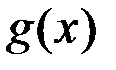 имеет в точке
имеет в точке  разрыв если…
разрыв если…
А) 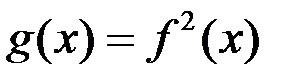
| *Б) 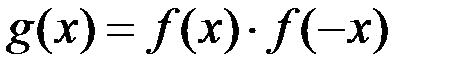
|
В) 
| Г) 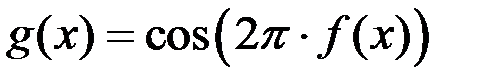
|
22.Дан график функции 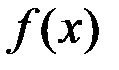
Тогда справедливо утверждение: функция 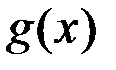 имеет в точке
имеет в точке  разрыв если…
разрыв если…
А) 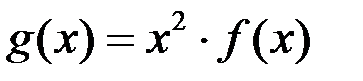
| *Б) 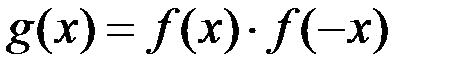
|
В) 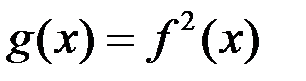
| Г) 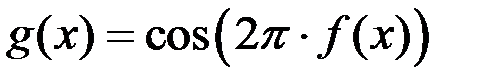
|
23.Дан график функции 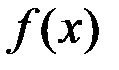
Тогда справедливо утверждение: функция 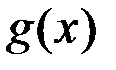 имеет в точке
имеет в точке  разрыв если…
разрыв если…
А) 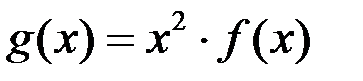
| *Б) 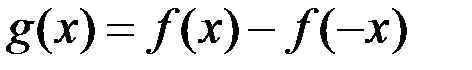
|
*В) 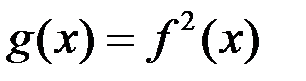
| *Г) 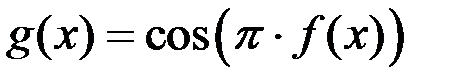
|
24.Дан график функции 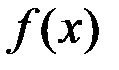
Тогда справедливо утверждение: функция 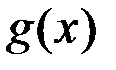 имеет в точке
имеет в точке  разрыв если…
разрыв если…
А) 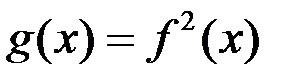
| Б) 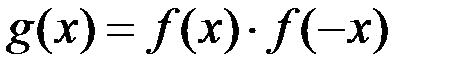
|
В) 
| *Г) 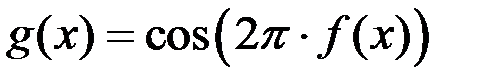
|
25.Пусть 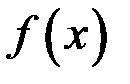 - непрерывная на всей оси функция. Тогда справедливо утверждение…
- непрерывная на всей оси функция. Тогда справедливо утверждение…
А) 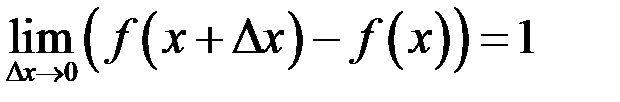
| *Б) 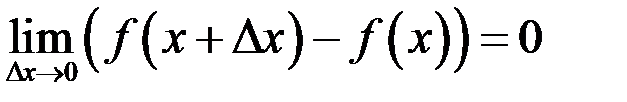
|
В) 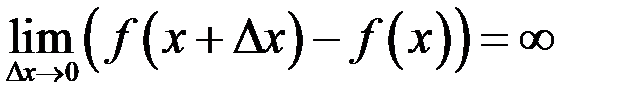
| Г) 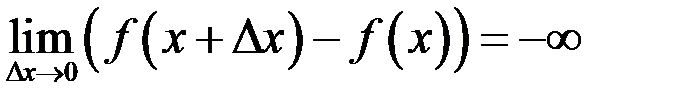
|
26.Пусть задана дифференцируемая в точке 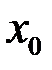 функция
функция 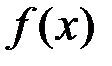 . Правильными утверждениями являются…
. Правильными утверждениями являются…
А) функция 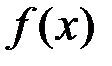 непрерывна в некоторой точке непрерывна в некоторой точке 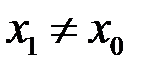
|
*Б) функция 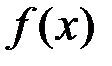 непрерывна в точке непрерывна в точке 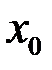 . .
|
В) функция 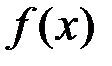 имеет в точке имеет в точке 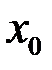 разрыв разрыв
|
Г) функция 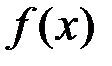 непрерывна в любой окрестности точки непрерывна в любой окрестности точки 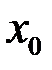 . .
|
27.Пусть задана непрерывная в точке 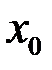 функция
функция 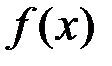 . Правильными утверждениями являются…
. Правильными утверждениями являются…
А) функция 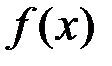 дифференцируема в некоторой точке дифференцируема в некоторой точке 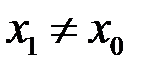 . .
|
Б) функция 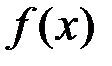 дифференцируема в точке дифференцируема в точке 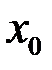 . .
|
В) функция 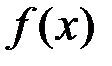 дифференцируема в любой окрестности точки дифференцируема в любой окрестности точки 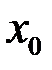 . .
|
*Г) функция 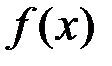 может иметь производную в точке может иметь производную в точке 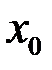 . .
|
28..Пусть на множестве 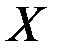 задана непрерывная функция
задана непрерывная функция  с множеством значений
с множеством значений 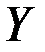 . Тогда на
. Тогда на 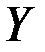 есть обратная к
есть обратная к 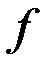 функция, если функция
функция, если функция 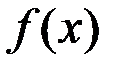 … .
… .
| А) имеет экстремум | Б) ограниченная |
| *В) монотонная | Г) периодическая. |
Часть 3. На каждое из заданий этой части Вы можете дать ответ в виде положительного или отрицательного числа.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|