
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пусть функция непрерывна в интервале , и , тогда наименьшее возможное число корней в этом интервале равно двум. Да.. Пусть функция непрерывна в интервале и , , , тогда наименьшее возможн
1) . Да.
2) . Нет.
3) . Да.
4) . Нет.
10.Верны ли утверждения?
1)Пусть функция непрерывна в интервале , и , тогда наименьшее возможное число корней в этом интервале равно двум. Да.
2)Пусть функция непрерывна в интервале и , , , тогда наименьшее возможное число корней в этом интервале равно пяти. Нет.
3)Может ли непрерывная в интервале функция, имеющая на концах интервала разные знаки, иметь в этом интервале ровно два корня. Нет.
4)Можно ли построить функцию, непрерывную во всех точках интервала 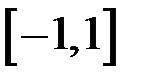 , за исключением одной точки
, за исключением одной точки  , отрицательную в точке
, отрицательную в точке 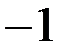 , положительную в точке
, положительную в точке 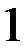 , но не имеющую корней. Да.
, но не имеющую корней. Да.
11.Пусть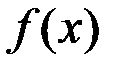 и
и 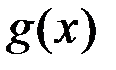 непрерывные в требуемых точках функции. Верны ли утверждения?
непрерывные в требуемых точках функции. Верны ли утверждения?
1)Если и , то . Да.
2)Если 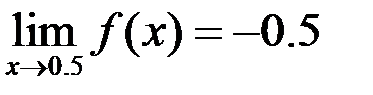 и
и 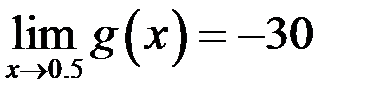 , то
, то
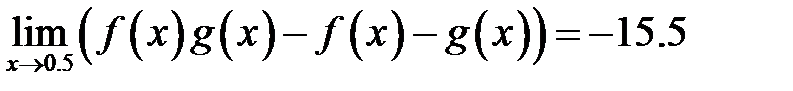 . Нет.
. Нет.
3)Если и , то . Да.
4) Если и , то . Нет.
5)Если и , то . Да.
6)Если 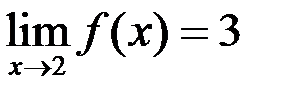 ,
, 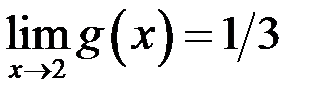 ,
, 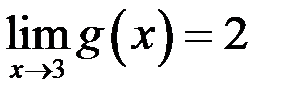 , то
, то 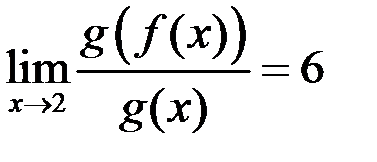 .
.
Да.
12.Верны ли утверждения?
1)В точке функция имеет неустранимый разрыв первого рода. Да
2)В точке 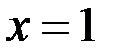 функция
функция 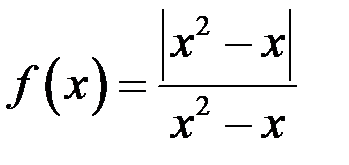 имеет устранимый разрыв первого рода. Нет(неустранимый разрыв первого рода)
имеет устранимый разрыв первого рода. Нет(неустранимый разрыв первого рода)
3)В точке 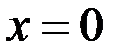 функция
функция 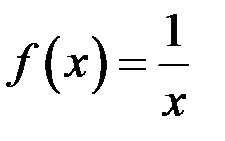 имеет разрыв первого рода. Нет(разрыввторого рода)
имеет разрыв первого рода. Нет(разрыввторого рода)
4)В точке функция имеет разрыв второго рода. Да
13.Верны ли утверждения?
1)Любая линейная комбинация непрерывных на отрезке функций является непрерывной функцией на этом отрезке. Да
2)Сумма двух непрерывных функций есть непрерывная функция. Да
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|