Хелпикс

Главная

Контакты

Случайная статья



Непрерывность функции.. Часть 1. Предлагаемые задачи, состоят из нескольких род­ст­вен­ных друг другу вопросов. На каждый из вопросов можно дать один из двух ответов: «Да» или «Нет».. Пусть функция  непрерывна в интервале ,  и , тогда наименьшее возможно

Стр 1 из 5Следующая ⇒


5. Непрерывность функции.

Часть 1. Предлагаемые задачи, состоят из нескольких род­ст­вен­ных друг другу вопросов. На каждый из вопросов можно дать один из двух ответов: «Да» или «Нет».

1.  Верны ли утверждения?

1)Пусть функция  непрерывна в интервале ,  и , тогда наименьшее возможное число корней в этом интервале равно двум.                                                                      Да.

2)Пусть функция  непрерывна в интервале  и , , , тогда наименьшее возможное число корней в этом интервале равно пяти.                                                                                                            Нет.

3)Непрерывная в интервале 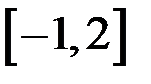 функция, имеющая на концах интервала разные знаки, может иметь в этом интервале ровно два корня.

                                                                                                                  Да.

4)Функцию, непрерывная во всех точках интервала 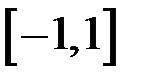, за исключением одной точки , отри­ца­тель­ная в точке 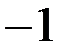, положительная в точке 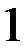, может не иметь корней на этом интервале.                            Да. 

2.Верны ли утверждения?

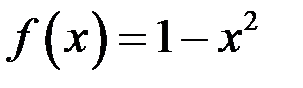1)Найдется такая окрестность точки , в которой функция  положительна.                                                                    Да. 

2)Если функции  и  определены в некоторой окрестности точки , то и функция  определена в окрест­ности точки .  Нет.

3)  Постоянная функция непрерывна везде.                                         Да.

4)  Тождественная функция , может не быть непре­рыв­ной в некоторой точке .                                                                                  Нет.

 

3.Функция 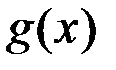  непрерывна в точке 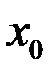. Тогда в точке  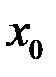непрерывна функция…

1) .         Да

2) .                   Нет

3)  .                     Да

4) . Нет

4.Пусть на отрезке 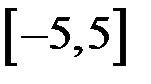 задана функция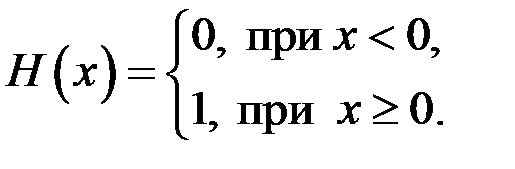   

Верны ли утверждения?


12345Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.