
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
координаты фокусов: .. Задача №9. Задача №10. Задача №11
координаты фокусов: .
Задача №9
Найти общее уравнение плоскости, проходящей через точки M1, M2 и M3, и расстояние от точки M0 до этой плоскости. Координаты точек M1, M2, M3 и M0:
M1 (– 1, 2, – 3), M2 (4, – 1, 0), M3 (2, 1, – 2), M0 (1, – 6, – 5).
Решение.
Уравнение плоскости, проходящей через точки М1 (-1,2,-3), М2 (4,-1,0), М3 (2,1,-2), запишется так:
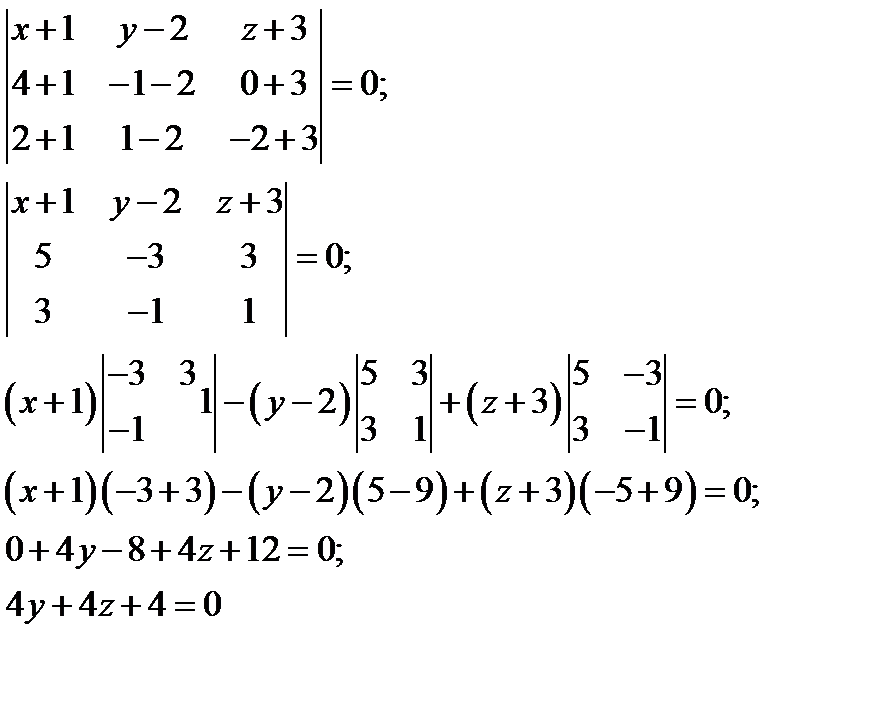
или 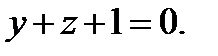
Найдем расстояние от точки М0 (1,-6,-5) до плоскости y + z +1 = 0:
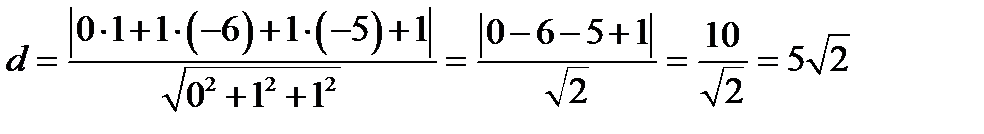
Ответ: уравнение плоскости 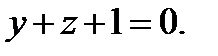
Расстояние от точки М0 до плоскости: d = 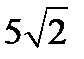
Задача №10
Найти канонические и параметрические уравнения прямой, заданной как пересечение двух плоскостей. Общие уравнения плоскостей, объединенные в систему: 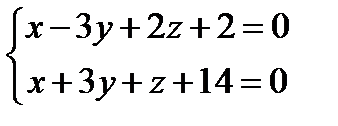
Решение.
В качестве направляющего вектора прямой возьмем векторное произведение нормалей данных плоскостей, т.е.  , где
, где
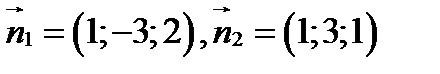 .
.
Тогда, 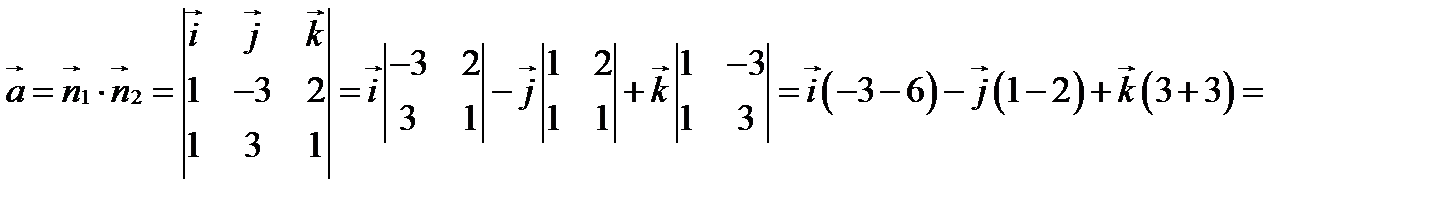
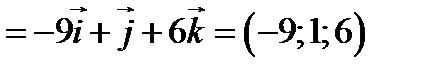 .
.
Возьмем какую-нибудь точку данной прямой. Полагаем z ≠ 0, значения x и y определяем из системы уравнений:
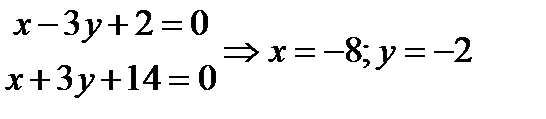
На прямой зафиксировали точку М0 (-8;-2;0).
Уравнения прямой запишутся так:
 – каноническое уравнение прямой;
– каноническое уравнение прямой;
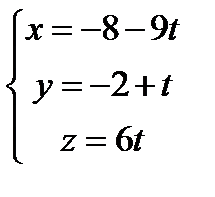 – параметрические уравнения прямой.
– параметрические уравнения прямой.
Ответ: каноническое уравнение прямой –  ;
;
параметрические уравнения прямой – 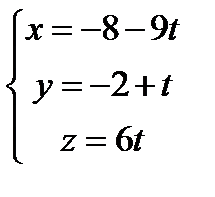 .
.
Задача №11
Найти угол между прямой и плоскостью. Если прямая и плоскость не параллельны, то найти точку их пересечения. Канонические уравнения прямых и общие уравнения плоскостей:
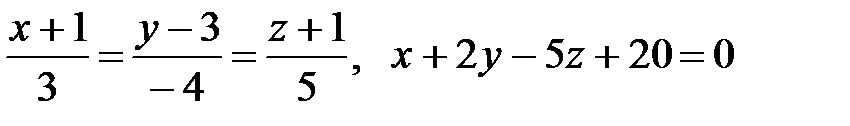 .
.
Решение.
Направляющий вектор данной прямой: 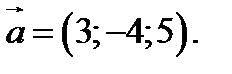
Нормальный вектор данной плоскости: 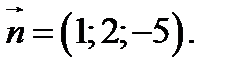
Синус угла между прямой и плоскостью найдем по формуле:
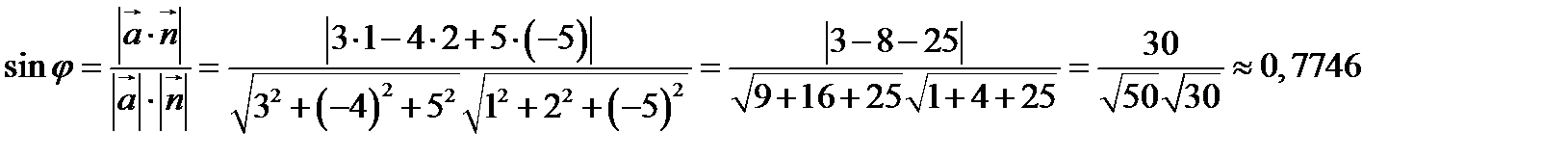 Тогда
Тогда 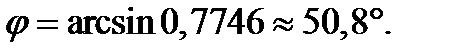
Найдем точку пресечения прямой и плоскости.
Запишем уравнение прямой в параметрическом виде:
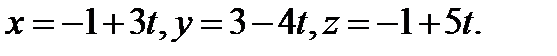 Подставим выражения для x, y, z в уравнение плоскости:
Подставим выражения для x, y, z в уравнение плоскости:
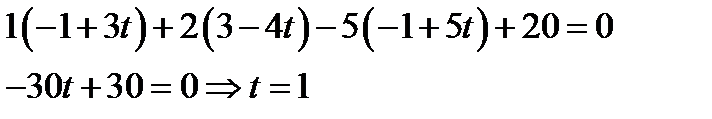
Из уравнения прямой получим координаты точки пересечения:
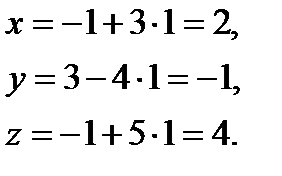
Точка М0 (2; -1; 4) – точка пересечения данных прямой и плоскости.
Ответ: угол пересечения прямой и плоскости 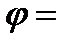
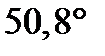 ;
;
точка пересечения – М0 (2; -1; 4).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|