Контакты

Случайная статья

Задача №4. Задача №5. Задача №6

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒

Задача №4

Вычислить площадь параллелограмма, построенного на векторах a и b. Выражения a и b через векторы p и q:

.

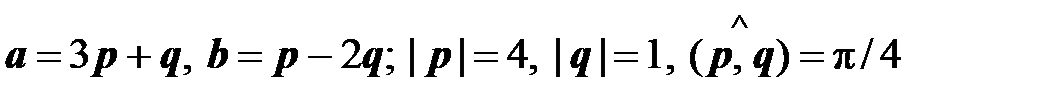Решение

Площадь параллелограмма, построенного на векторах 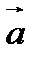и 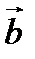находится по формуле:

.

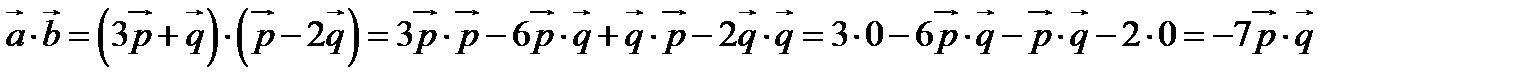Следовательно, S = 14 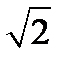(квадратных единиц)

Ответ: S = 14 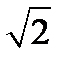(квадратных единиц).

Задача №5

Компланарны ли векторы a, b и c? Координаты векторов a, b и c: .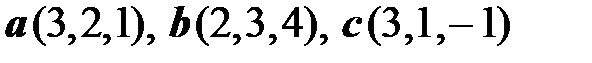

Решение

Векторы 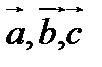компланарны, если их смешанное произведение равно нулю. Проверим это условие.

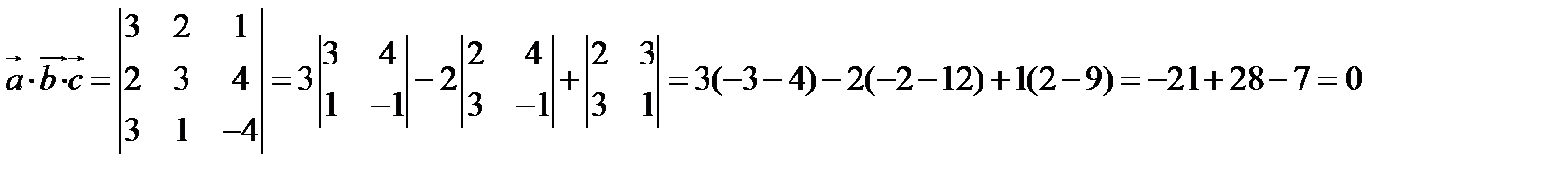Следовательно, векторы 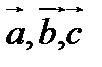компланарны.

Ответ: векторы 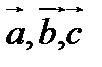компланарны.

Задача №6

Исследовать систему линейных алгебраических уравнений на совместность и решить 1) методом Гаусса, 2) по правилу Крамера в случае единственности решения, 3) матричным методом в случае единственности решения. Системы уравнений: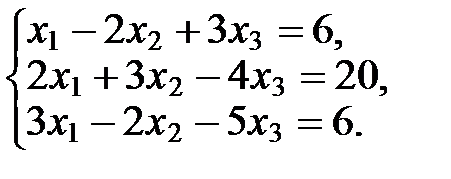

1). Решим данную систему методом Гаусса.

Запишем рассмотренную матрицу и с помощью элементарных преобразований над строками матрицы упростим её:

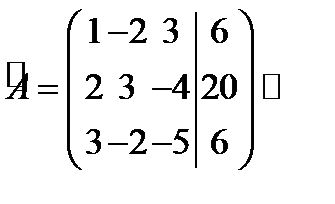
из 2-й строки вычтем 1-ю, умноженную на 2; из 3-й строки вычтем 1-ю, умноженную на 3:

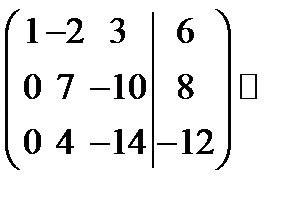
из 3-й строки, умноженной на 7, вычтем 2-ю строку, умноженную на 4:

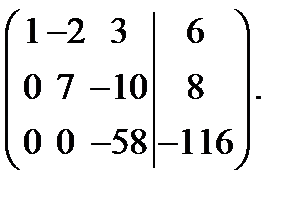
Последней матрице соответствует следующая система уравнений, эквивалентная исходной:

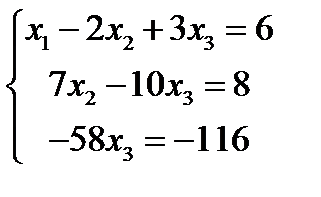
Из 3-го уравнения получим:

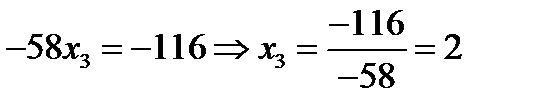
Из 2-го уравнения:

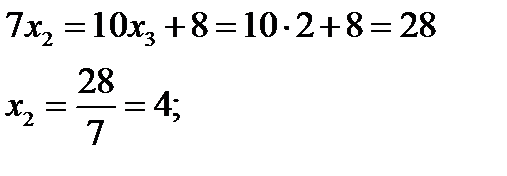
Из 1-го уравнения:

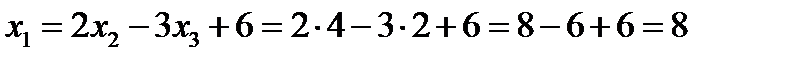
Решение системы:

x₁=8; x₂=4; x₃=2.

2). Решим систему по формулам Крамера:

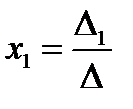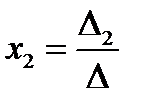, и .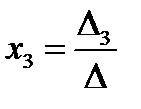

Посчитаем определитель системы:

Так как определитель системы Δ отличен от нуля, то система совместна и имеет единственное решение.

Находим :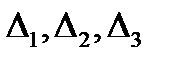

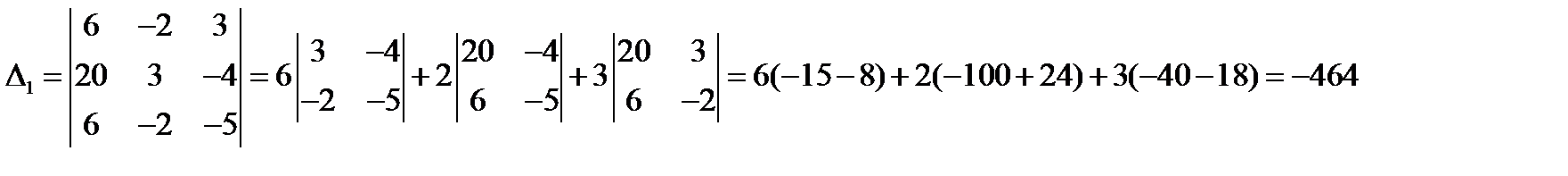
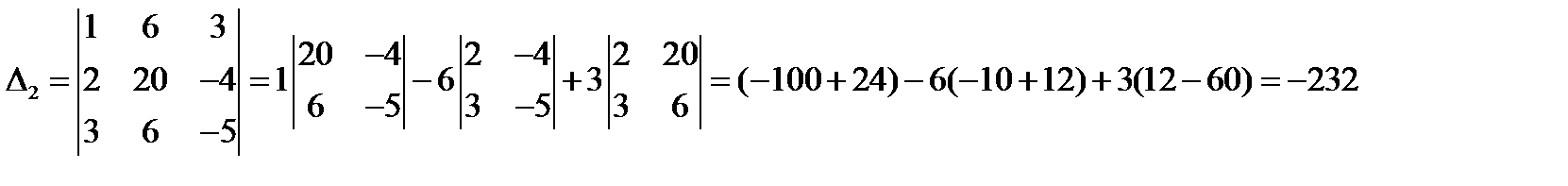
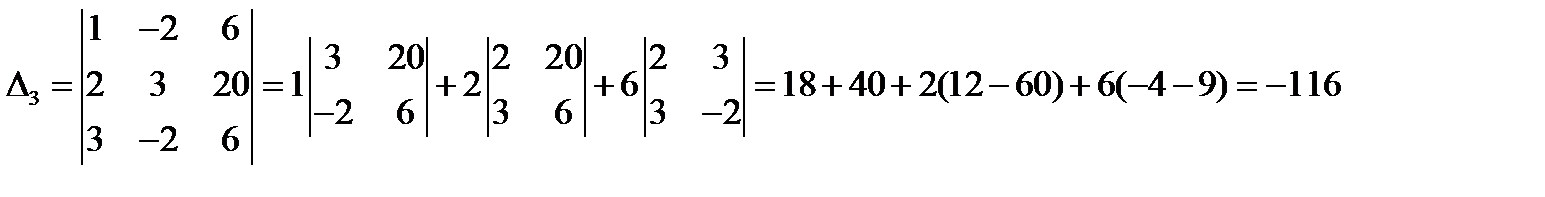
Тогда,

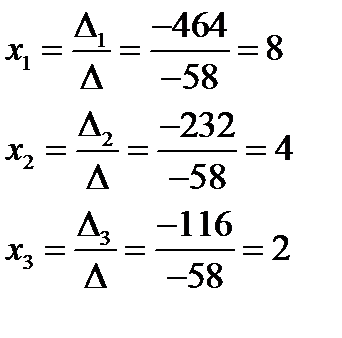
3). Запишем систему в матричном виде:

АХ=В, где

Решение системы будет:

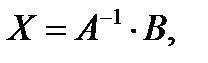где 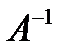– матрица обратная матрице А

где А_ij – алгебраические дополнения элементов a_ij матрицы А.

из пункта 2) равно -58.

Находим алгебраическое дополнения:

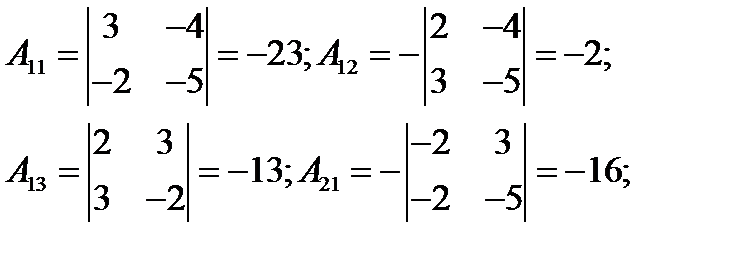
Тогда,

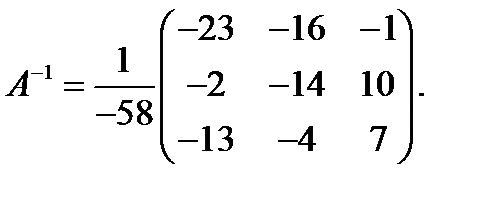
Следовательно,

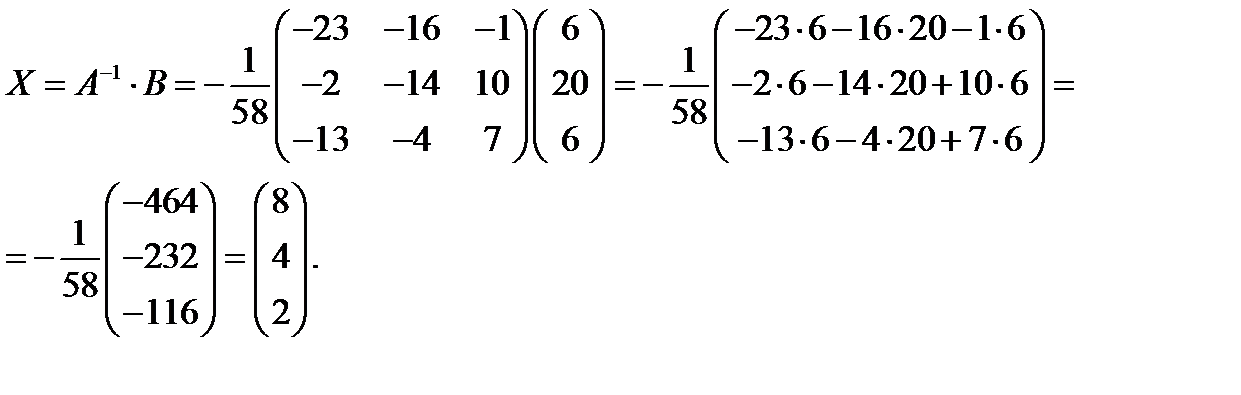
Решение системы: х₁ = 8, х₂ = 4, х₃ = 2.

Ответ: х₁ = 8, х₂ = 4, х₃ = 2.

⇐ Предыдущая 123 4 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.