Хелпикс

Главная

Контакты

Случайная статья



Задача №7. Задача №8

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒


Задача №7

На плоскости OXY найти общие уравнения прямых, проходящих через точку пересечения двух прямых перпендикулярно первой и параллельно третьей соответственно. Общие уравнения трех прямых на плоскости OXY даны ниже в соответствии с вариантом. Уравнения двух первых прямых объединены в систему:

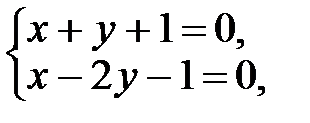  x – 2y – 2 = 0.

Решение.

Сначала находим точку пересечения прямых:

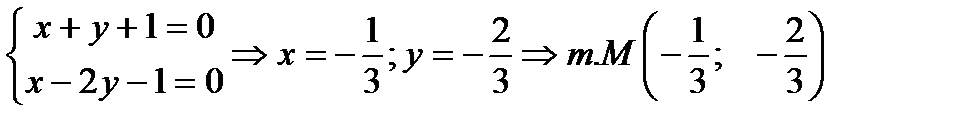 – это точка пересечения прямых.

Запишем уравнение первой прямой: x+y+1=0. Уравнение прямой перпендикулярной первой, имеет вид: x-y+c=0. Точка М 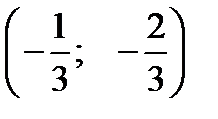 лежит на этой прямой, значит её координаты должны удовлетворять этому уравнению: .

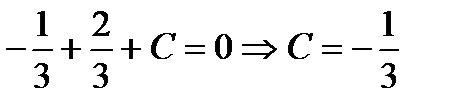Уравнение прямой принимает вид: x – y – 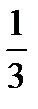= 0

Уравнение прямой, параллельной прямой x – 2y – 2 =0 имеет вид:

 x – 2y + C = 0.

Для определения С подставим координаты точки М:

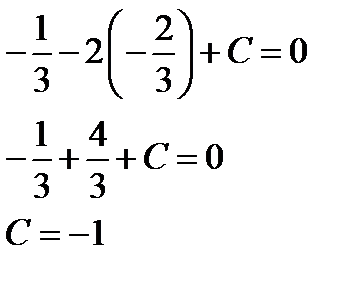
Уравнение прямой принимает вид x – 2y – 1 = 0.

Ответ: Уравнение x – 2y – 1 = 0.

 

Задача №8

Приведением уравнения к каноническому виду установить, что оно определяет эллипс, гиперболу или параболу. Построить соответствующую кривую 2-го порядка на плоскости OXY. Для эллипса и гиперболы найти полуоси, координаты фокусов, эксцентриситет, уравнения директрис. Найти уравнения асимптот гиперболы. Для параболы найти параметр, координаты фокуса, уравнение директрисы. Уравнения кривых:

3x2 + 4y2 = 12.

Решение.

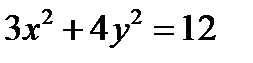, разделим на 12:

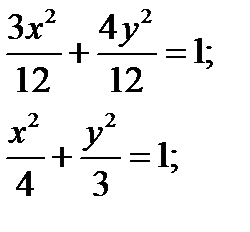
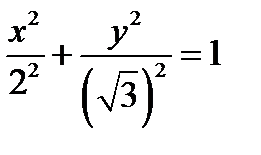– каноническое уравнение эллипса.

Большая полуось а = 2, малая полуось b = .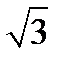

Координаты фокусов: F1 (-c;0), F2 (c;0), где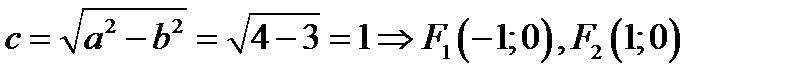

Эксцентриситет эллипса равен:

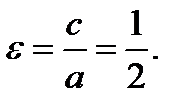
Директрисы эллипса это прямые, уравнения которых

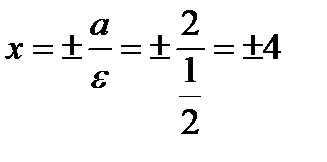
Построим данный эллипс:

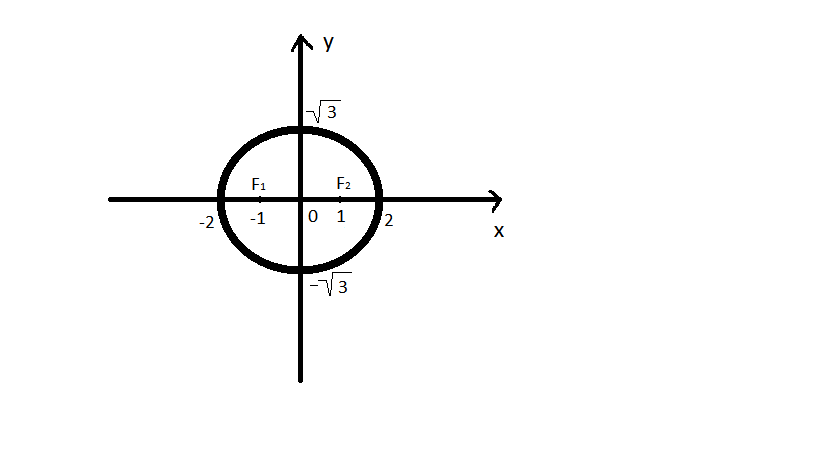
Ответ: 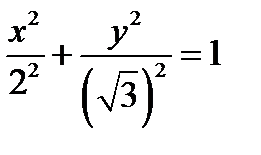– каноническое уравнение эллипса;

большая полуось а = 2, малая полуось b = ;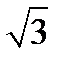

 

эксцентриситет эллипса равен:

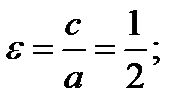
директрисы эллипса: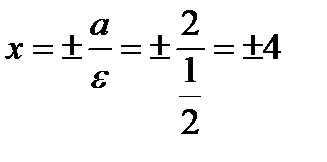


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.