
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение задач по определению физических зависимостей
2.3. Решение задач по определению физических зависимостей
Задача 2.3
Оценить скорость распространения звука в воздухе при нормальных условиях, т. е. давлении 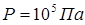 , плотности
, плотности 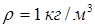 .
.
Скорость распространения звука в воздухе зависит в основном от 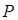 и
и 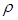 . При этом функциональная зависимость имеет вид
. При этом функциональная зависимость имеет вид
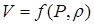 . (2.22)
. (2.22)
Запишем функциональную связь (2.22) в явной форме в виде алгебраического соотношения
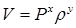 . (2.23)
. (2.23)
Размерности величин, входящих в (2.33) имеют вид: 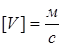 ;
; 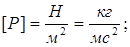
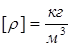 .
.
Подставив размерности в уравнение (2.23), получим
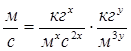 .
.
После преобразования имеем
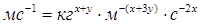 . (2.24)
. (2.24)
Приравняв показатели степеней однородных величин левой и правой части уравнения (2.24), получим систему из трех алгебраических уравнений:
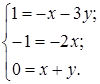 (2.25)
(2.25)
Решая систему уравнений, находим: 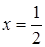 ;
; 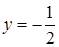 .
.
Третье уравнение в системе свидетельствует о том, что х равен у с обратным знаком. Подставляя полученные значения х и у в (2.33), получаем решение задачи
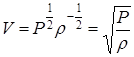 . (2.26)
. (2.26)
Проведем численные расчеты, подставив в уравнение (2.26) значения величин
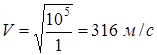 .
.
Преобразуем выражение (2.26), воспользовавшись уравнением Менделеева-Клапейрона
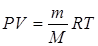 ,
,
и найдем плотность газа
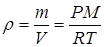 . (2.27)
. (2.27)
Подставив (2.27) в (2.26) получим
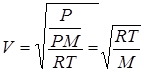 . (2.28)
. (2.28)
Более точное выражение для определения скорости звука в газах имеет следующий вид
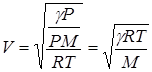 , (2.29)
, (2.29)
где 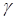 — показатель адиабаты, который зависит от вида газа и принимает значение в интервале 1,3…1,5.
— показатель адиабаты, который зависит от вида газа и принимает значение в интервале 1,3…1,5.
Отличие формулы (2.28) от теоретической формулы (2.29) в 1,14…1,22 раза является незначительным. Но это разница может быть учтена, введя коэффициент пропорциональности k в формулу (2.23),
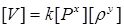 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|