Контакты

Случайная статья

ПЗ: Методология исследовательской деятельности в машиностроении

Стр 1 из 4Следующая ⇒

ПЗ: Методология исследовательской деятельности в машиностроении

Для гр. КТПм-19-о на 01.04.2020г.

(дистанционное обучение)

Задачи по разделу 2. ФИЗИЧЕСКОЕ МОДЕЛИРОВАНИЕ

В данном разделе приводится набор задач, решаемых методом размерностей, который является основой физического моделирования. Рассмотрены примеры решения задач-оценок и задач по выводу формул физических зависимостей.

2.1. Решение задач по оценке величины

Задача 2.1

Оценить скорость опускания парашютиста с раскрытым парашютом, если масса парашютиста m=75 кг, радиус парашюта равен r=3 м. Плотность воздуха при нормальных условиях равна r= кг/м³.

Для решения задачи проанализируем характер равномерного движения парашютиста в воздухе с раскрытым парашютом. На рисунке 2.1 изображена схема движения парашютиста и силы, действующие на него.

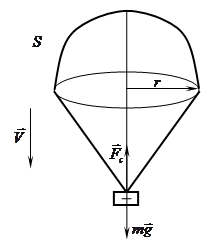
Рисунок 2.1 — Схема движения парашютиста к решению задачи 2.1

За время 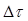на парашют площадью S налетает со скоростью V воздух, имеющий массу , и придает парашютисту импульс .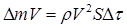

Сила сопротивления воздуха согласно второму закону динамики

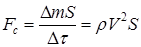. (2.1)

При установившемся (равномерном) движении сила сопротивления уравновешивается силой тяжести парашютиста и согласно второму закону Ньютона: . Поэтому

. (2.2)

Из (2.2) находим

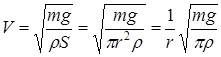. (2.3)

Подставим в (2.3) численные значения и получим решение задачи:

.

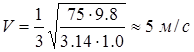Теперь решим эту задачу с помощью метода размерностей.

Очевидно, что сила сопротивления зависит от плотности воздуха 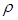, скорости движения парашютиста 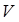и от площади парашюта .

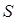Запишем функциональную связь

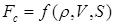. (2.4)

Выразим функцию (2.4) в явной форме в виде алгебраического соотношения

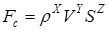, (2.5)

где х, y ,z — показатели степеней, которые необходимо определить.

Запишем размерность единиц физических величин, входящих в (2.5) 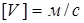, , 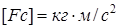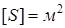подставив в (2.5), получим

.

Преобразуем данное соотношение к виду

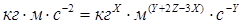. (2.6)

Приравнивая показатели степеней однородных физических величин левой и правой частей уравнения (2.6), получаем систему уравнений

(2.7)

Решая систему уравнений с тремя неизвестными, определяем

Подставляя значения X, Y, Z в (2.5), получаем

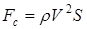. (2.8)

Приравняем правые части выражений (2.8) и (2.2)

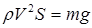. (2.9)

Из (2.9) находим решение задачи

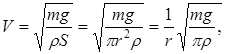(2.10)

из которого видно, что выражения (2.10) и (2.3) полностью совпадают.

12 3 4 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.