
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Функция двух случайных величин. Распределение суммы независимых слагаемых.
§…Функция двух случайных величин. Распределение суммы независимых слагаемых.
Опр. Если каждой паре возможных значений случайных величин Х и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов X и Y : Z = φ(X, Y).
Рассмотрим в качестве такой функции сумму Х + Y. В некоторых случаях можно найти ее закон распределения, зная законы распределения слагаемых.
1) Если X и Y – дискретные независимые случайные величины, то для определения закона распределения Z = Х + Y нужно найти все возможные значения Z и соответствующие им вероятности.
Пример 4. Рассмотрим дискретные случайные величины X и Y, законы распределения которых имеют вид:
Х -2 1 3 Y 0 1 2
р 0,3 0,4 0,3 р 0,2 0,5 0,3
Найдем возможные значения Z: -2 + 0 = -2 ( р = 0,3·0,2 = 0,06), -2 + 1 = -1 (р = 0,3·0,5 = 0,15), -2 + 2 = 0 (р = 0,3·0,3 = 0,09), 1 + 0 = 1 (р = 0,4·0,2 = 0,08), 1 + 1 = 2 (р = 0,4·0,5 = 0,2), 1 + 2 = 3 (р = 0,4·0,3 = 0,12), 3 + 0 = 3 (р = 0,3·0,2 = 0,06), 3 + 1 = 4 (р = 0,3·0,5 = 0,15), 3 + 2 = 5 (р = 0,3·0,3 = 0,09). Сложив вероятности повторившегося дважды значения Z = 3, составим ряд распределения для Z:
| Z | -2 | -1 | ||||||
| р | 0,06 | 0,15 | 0,09 | 0,08 | 0,2 | 0,18 | 0,15 | 0,09 |
3) Если X и Y – непрерывные независимые случайные величины, то, если плотность вероятности хотя бы одного из аргументов задана на (-∞, ∞) одной формулой, то плотность суммы g(z) можно найти по формулам
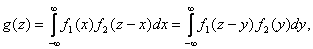
где f1(x), f2(y) – плотности распределения слагаемых. Если возможные значения аргументов неотрицательны, то
g(z)= 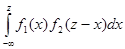
Замечание. Плотность распределения суммы двух независимых случайных величин называют композицией.
Устойчивость нормального распределения.
Опр. Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон (возможно, отличающийся другими значениями параметров).
В частности, свойством устойчивости обладает нормальный закон распределения: композиция нормальных законов тоже имеет нормальное распределение, причем ее математическое ожидание и дисперсия равны суммам соответствующих характеристик слагаемых.
§… Неравенство Чебышева.
Пусть Х – непрерывная случайная величина
М[Х]=a
Задача: оценить 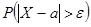
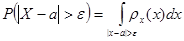
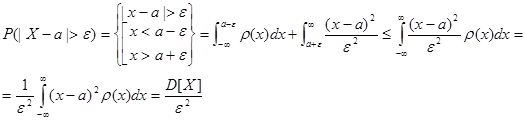
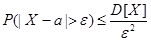
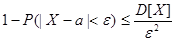
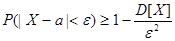
Вероятность того, что отклонение случайной величины X от ее математического ожидания по абсолютной величине меньше любого положительного числа ε не менее, чем 1-D[x]/ε2.
Замечание:
Доказательство проведено для непрерывных случайных величин. Неравенство Чебышева справедливо и для дискретных случайных величин (доказательство аналогично).
§… Теорема Чебышева.
1. пусть X1, X2, …. Xn – попарно-независимые случайные величины с какими угодно распределениями.
2. M[Xk]=ak
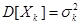 , k=1, 2….n
, k=1, 2….n
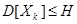
3. 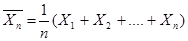
Тогда 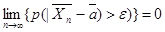

Где 
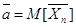
Доказательство:
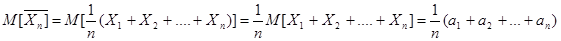
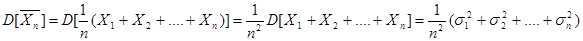
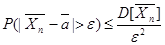

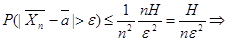

Замечание:
Математические теоремы, в которых выясняются закономерности поведения суммы большого числа случайных величин, а также условия их возникновения, получили общее название закона больших чисел.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|