
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс.
§…. Оценка отклонения теоретического распределения от нормального. Асимметрия и эксцесс.
Опр: Начальным моментом порядка k случайной величины Х называю мат.ожидание случайной величины Хk .
ν к= М[Xk] k= 1, 2, 3 ….
ν1= МХ
ν2=М[Х2]
DХ= ν2- ν12
Опр: Центральным моментом порядка k случайной величины Х называют мат.ожидание случайной величины (Х-МХ) k
µk= М[(Х-МХ) k]
µ1=0
µ2= DХ
Пусть ρ(х) – симметричная функция относительно х=МХ, тогда любой центральный момент нечетного порядка будет равен 0., а для несимметричной функции ρ(х) момент не равен 0.
Тогда очевидно µk (k=2n+1) может служить мерой асимметричности распределения.
Опр: Асимметрией теоретического распределения называется отношение дка к кубу среднеквадратичного отклонения :
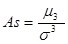
Для нормального распределения As=0
As>0 , если большая часть кривой справа от МХ. As<0, если большая часть кривой слева от МХ.
Вместо МХ на практике используют моду распределения –максимум на кривой плотности распределения.
Опр: Эксцессом называют характеристику, определяемую равенством Ек= 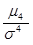 -3
-3
Для нормального распределения 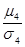 =3
=3
§…Распределение функции одного случайного аргумента.
Пусть Х – случайна величина. Если каждому возможному значению Х соответствует одно возможное значение случайной величины Y, то Y – функция случайного аргумента Х.
Y=φ(Х)
1)Х – дискретная случайна величина, Y=Х2
| хi | - 2 | ||
| рi | 0,4 | 0,5 | 0,1 |
| уi | ||
| рi | 0,9 | 0,1 |
Вероятности соответствующих значений Х и У Y равны, если двум значениям Х соответствует одно значение Y, то соответствующие вероятности складываются.
2)Х – непрерывная случайная величина.
Х→ρ(х) Y =ψ(Х)
Если Y =φ(Х) – дифференцируемая, строго убывающая или строго возрастабщая функция, обратная которой Х= ψ (Y). Тогда плотность распределения случайной величины Y вычисляется по формуле: ρу(у)= ρх(ψ (y)) |ψ´(у)|
Пример:
Пусть Х→N(0,σ) , Y =Х3
ρх(х)= 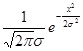
Y =φ(Х)=Х3 , Х=3 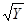 =ψ (Y)
=ψ (Y)
ρу(у)= 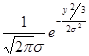 .
. 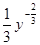
Х→N(а,σ) У=АХ+В
y=φ(х)=Ах+В, х= 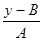 =ψ(у)
=ψ(у)
ρу(у)= 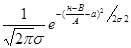 |
| 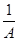 |=
|= 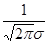
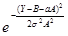 =
= 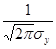
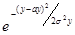
М[Y]=В+аА
σу=σ|A|
Х – дискретная случайная величина Y =φ(Х)
М[Y]= 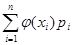
Х – непрерывная случайная величина
М[Y]= 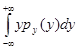 =
= 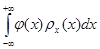
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|