Контакты

Случайная статья

ЛЕКЦИЯ 10 - 15.04.2014

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

ЛЕКЦИЯ 10 - 15.04.2014

§ 4. Элементы теории поля.

Определение векторного поля.

Векторная функция, отображающая .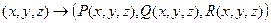

Градиент скалярной функции - векторная функция: , ,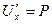

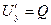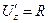
Пример: 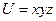- тогда .

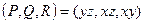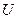называется потенциалом поля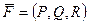

Потенциальное поле: Если существует такая U(x,y,z), что 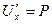, , 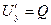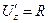(то есть их общая первообразная), векторное поле называется потенциальным, U(x,y,z) - его потенциал.

Свойство. Если U - потенциал, то U+C - тоже потенциал.

Доказательство: , ,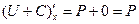

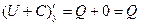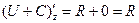
Теорема 1. Поле F потенциально 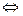симметрична производная матрица .

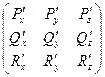ДОКАЗАТЕЛЬСТВО.

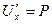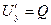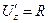, , , тогда

=

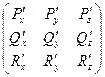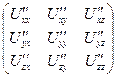
потому что , ,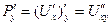

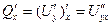Но (!!!) эти смешанные частные производные 2-го порядка совпадают, значит, = .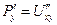

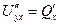Аналогично 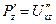= 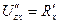. Аналогично = .

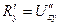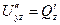Итак, 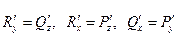и матрица симметрична.

Определение. Дивергенция векторного поля.

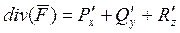(сумма элементов главной диагонали производной матрицы).

Определение Ротор векторного поля.

rot(F) = = .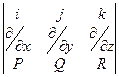

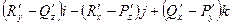Куда направлен ротор (чертёж на доске для векторного поля (-y,x,0) ).

Определение. Если ротор = 0 то поле называется безвихревым.

Следствие. Векторное поле F потенциально 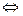его ротор = 0.

ДОКАЗАТЕЛЬСТВО.

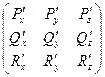симметрична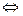

= .

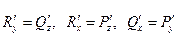
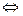
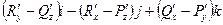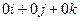Следствие (для плоского поля). Векторное поле в R² потенциально .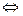

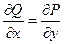Определение. Работа векторного поля при перемещении точки по замкнутому контуру называется циркуляцией.

Обозначение: 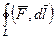или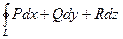

ЛЕММА. Криволинейный интеграл 2 рода от F не зависит от пути 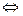циркуляция = 0.

ДОКАЗАТЕЛЬСТВО.

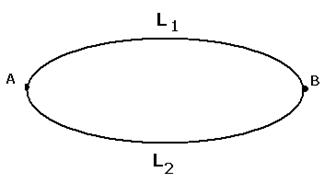
Необходимость.

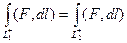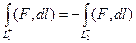Если то то .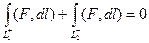

Но так как объединение 2 частей в замкнутый контур 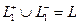, тогда и получается

.

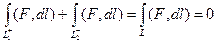Достаточность.

Если 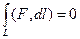, разобъём контур на 2 части какими-нибудь 2 точками А,В.

Возникают 2 части, и 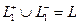, тогда 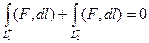, значит 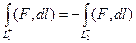значит 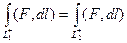. Что и требовалось доказать.

⇐ Предыдущая 1 234 Следующая ⇒

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.