ЛЕКЦИЯ 8 - 01.04.2014

ЛЕКЦИЯ 8 - 01.04.2014

Глава 4.

§ 1. Кратные интегралы.

Определение. Геометрический и физический смысл.

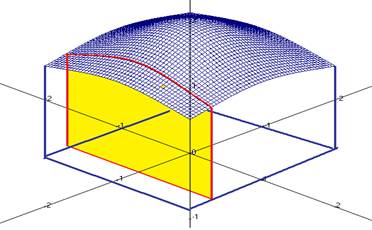
Кратные интегралы, двойные, тройные. Свойства. Вычисление двойных интегралов по прямоугольной и не-прямоугольной области. Геометрический смысл. Объём фигуры под поверхностью.

Сведение к повторным: интегрирование величин всех площадей криволинейных трапеций в сечениях по перпендикулярному направлению.

Смена порядка интегрирования:

Вычисление тройных интегралов.

Примеры.

Аналогично, массив в программировании может быть не прямоугольным, тогда во внутреннем цикле двойного цикла границы переменные и зависят от переменной, определённой во внешнем цикле:

for i : = 1 to 10 do

for j : = 1 to i do

read (a[i,j]);

end; end;

Приложения кратных интегралов.

Вычисление площадей фигур и объёмов тел.

Вывод формулы площади поверхности.

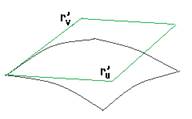
Площадь каждого такого параллелограмма вычисляется с помощью векторного

произведения: .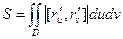

Формула для явно заданной поверхности: .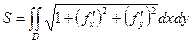

§ 2. Замена переменных в кратных интегралах.

Полярные координаты на плоскости.

Вывести формулы перехода к полярным координатам на плоскости:

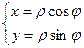Определитель Якоби: .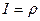

При замене двух старых на две новые переменные в плоскости, существует уже 4 различных частных производных, и из них можно образовать матрицу 2-го порядка.

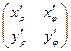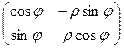
Её определитель: = .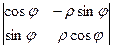

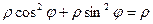На этот определитель нужно домножить в кратном интеграле после пересчёта всех переменных.

Геометрический смысл определителя Якоби - правильный учёт искажений (деформаций).

Чертёж - слева в плоскости параметров 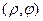, справа в плоскости .

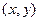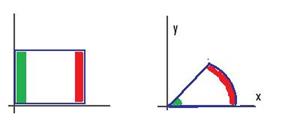
При одном и том же угле поворота, площади секторов, находящихся дальше от центра, будут больше, чем те, которые ближе к центру. Если бы не умножали на определитель Якоби, то влияние значений функции в этих секторах было бы одинаковым, так как диапазон изменений угла для них один и тот же.

Определитель Якоби в кратных интегралах имеет точно такой же смысл, как например дополнительный множитель, появляющийся при заменен переменной в неопределённом или определённом интеграле. Так, если 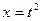, то при замене пишем 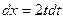. Множитель 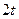фактически и является одномерным якобианом, но только для матрицы порядка 1 определитель вычислять было не нужно, так как он совпадает с самим этим элементом.

12 3 4 Следующая ⇒