Хелпикс

Главная

Контакты

Случайная статья



ЛЕКЦИЯ 9 - 08.04.2014

⇐ ПредыдущаяСтр 2 из 4Следующая ⇒


ЛЕКЦИЯ 9 - 08.04.2014

Продолжение - тема полярные координаты.

Пример: Вычислить интеграл 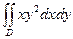 где D -  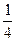часть круга единичного радиуса в первой четверти плоскости.

Решение.  =  =  =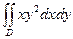

 =  =  =

 =  =

 

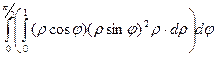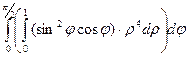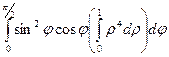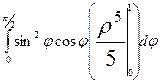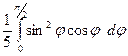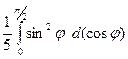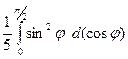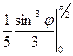
Пример: Доказать формулу площади круга с помощью полярных координат.

 =  =  =  =  = .

 

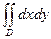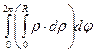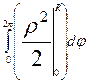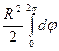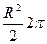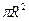Цилиндрические и сферические координаты в пространстве.

Существует два различных обобщения полярных координат для трёхмерного пространства.

Вывод формул перехода к цилиндрическим координатам в пространстве:

.

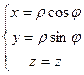Вычислить определитель Якоби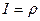

Задача: доказать формулу объёма конуса

 

Вывод формул перехода к сферическим координатам:

Вывести формулы перехода к сферическим координатам в пространстве:

.

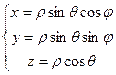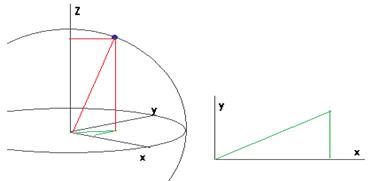
Вычислить определитель Якоби .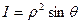

Пример: доказать формулу объёма шара с помощью перехода к сферическим координатам.

 

Задача: доказать формулу объёма шара с помощью тройного интеграла и сферических координат.

 

§ 3. Криволинейные и поверхностные интегралы от векторных функций.  

Определение. Свойства, геометрический и физический смысл. Работа силы по перемещению точки по кривой, поток поля через поверхность.

Вывод формул вычисления для явно заданной кривой, поверхности.

Пример (набрать).


⇐ Предыдущая1234Следующая ⇒
  

© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.