ordm; Производственная функция фирмы

29º Производственная функция фирмы

Пусть фирма производит один вид продукции, используя несколько видов затрат (ресурсов). В этом случае она должна выбрать точку в пространстве ресурсов, которое состоит из всех возможных комбинаций затрат. В предположении, что все затраты могут непрерывно изменяться (безгранично делимы), пространство ресурсов будет представлять собой неотрицательный ортант пространство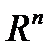

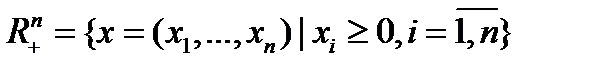
Величина 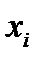- количество ресурсов, используемое фирмой.

Технологическая связь между выпуском продукта и затратами называется производственной функцией. Математически это понятие можно определить следующим образом.

Неотрицательную функцию 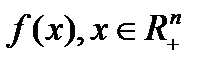называют производственной функцией, если:

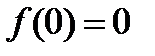
2. 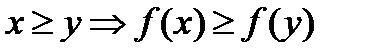(совокупность покомпонентных неравенств)

3. Вогнута по каждому аргументу.

Величина 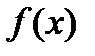может представлять собой либо физический объём выпущенной продукции при выбранной единице ее измерения, либо доход фирмы, т.е. стоимость произведенной продукции.

Первое требование к производственной функции является отражением того факта, что невозможно произвести продукцию без затрат. Второе требование также прозрачно: увеличение затрат не может привести к уменьшению выпуска продукции.

Далее считаем, что имеет непрерывные частные производные по каждому аргументу в тех точках, в которых эти производные имеют смысл (не имеет смысл для тех, у которых i-тая компонента равна нулю, мы можем говорить тогда об односторонних. Но, вообще говоря, и односторонние могут быть не определены).

Пусть 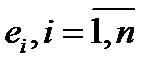- единичный вектор (орт) пространства , у которого 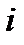-тая компонента равна 1, 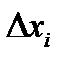- приращение -го ресурса, 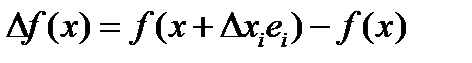- соответствующее приращение выпуска продукции. Величина 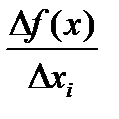, показывающая прирост выпуска на единицу прироста 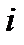-го ресурса, называется производительностью 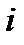-го ресурса в точке .

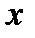Величину 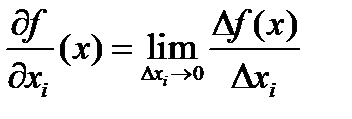называют предельной производительностью i-го ресурса или предельным продуктом по i-му ресурсу. Из второго условия, наложенного на производственную функцию, следует, что все продукты неотрицательны.

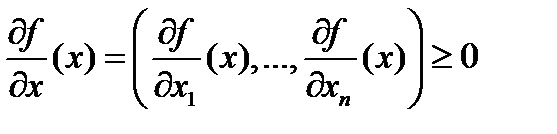
Третье условие связано с законом об убывающей доходности (см. п5). Оно выполняется тогда и только тогда, когда 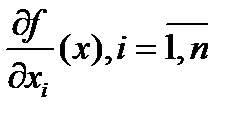не возрастает по i-му агрументу. Это означает, что последовательное увеличение любого вида затрат может привести только к уменьшению предельного продукта, то есть к меньшему приросту производственной функции.

Примеры производственной функции:

1. Линейная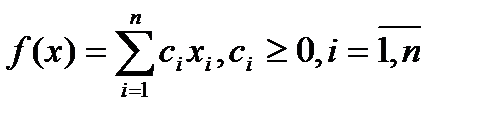

2. ПФ Кобба-Дугласа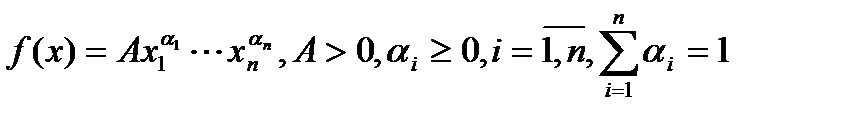

3. ПФ Леонтьева: .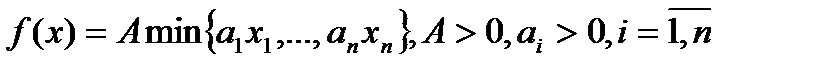

Пусть с целью расширения производства фирма увеличивает все виды затрат в 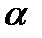раз, тогда относительный прирост производства составит: 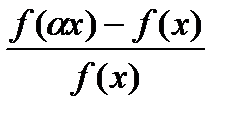где 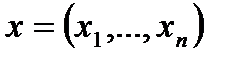вектор первоначальных затрат фирмы.

При этом относительное увеличение каждого вида затрат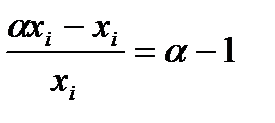

Величина (1) 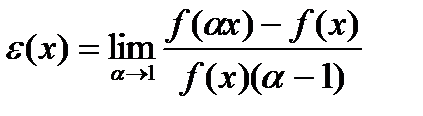является локальным показателем увеличения выпуска продукции при расширении масштабов производства и называется эластичностью производства.

Легко видеть ,что эластичность >=0. Если она >1(<1), то при пропорциональном расширении пространства выпуск продукции возрастает в большей (меньшей) степени, чем затраты.

Заметим, что 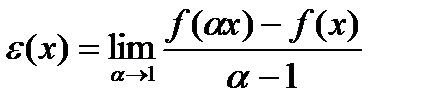=[можно представить как]= 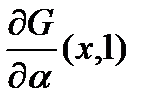, где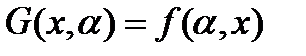

Т.к. 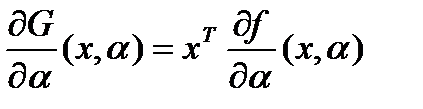, то эластичность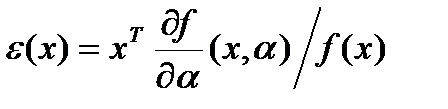

Определим эластичность выпуска по отношению к i-му ресурсу следующим образом:

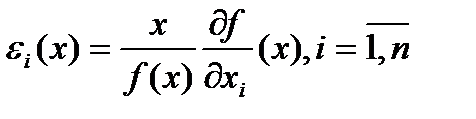(2)

Легко видеть, что 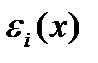есть предел отношения относительного увеличения выпуска продукции к относительному приращению i-го вида затрат, когда это приращение стремиться к нулю, а другие затраты не изменяются.

Из формул (1),(2) получаем:

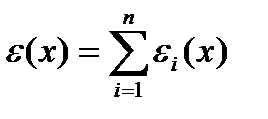
Таким образом, эластичность производства равна сумме эластичностей выпуска по отношениям ко всем ресурсам.

Замечание: Иногда при моделировании производства ограничиваются двухфакторными ПФ 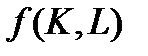, где 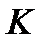- затраты капитала, 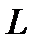- затраты трудовых ресурсов.

ПФ такого типа часто используется в макроэкономике. На микроуровне (при большей детализации) модели с двухфакторными ПФ-ми могут быть грубыми.

⇐ Предыдущая 19 20 21 22 23 24 25 262728 Следующая ⇒