
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ordm; Моделирование запаздывания при освоении капиталовложений
26º Моделирование запаздывания при освоении капиталовложений
При моделировании экономических процессов часто приходится иметь дело с эффектом запаздывания. Так, например, сделанные в некоторый момент времени инвестиции не могут мгновенно превратиться в фонды. Имеется два подхода к моделированию запаздывания в процессе освоения капиталовложений. Первый из них предполагает наличие временного промежутка лага 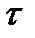 , по прошествии которого капиталовложения превращаются в фонды. В этом случае можно считать, что фонды, входящие в строй в году
, по прошествии которого капиталовложения превращаются в фонды. В этом случае можно считать, что фонды, входящие в строй в году 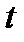 , созданы за счет инвестиций, сделанных в году
, созданы за счет инвестиций, сделанных в году 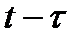 . Тогда уравнение движения фондов будет иметь вид
. Тогда уравнение движения фондов будет иметь вид  , где
, где 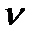 - коэффициент выбытия фондов.
- коэффициент выбытия фондов.
Непрерывным аналогом этой формулы является следующее дифференциальное уравнение с постоянным запаздыванием 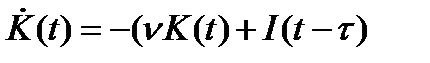
Наряду с данной моделью в настоящее время используется другой подход к моделированию запаздывания, основанный на введении так называемого распределённого лага. Суть этого подхода состоит в предположении, что инвестиции осваиваются постепенно. Конкретнее: если в году 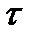 сделаны инвестиции
сделаны инвестиции 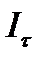 , то в году
, то в году 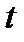 будет освоена часть
будет освоена часть 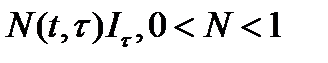 . Рассмотрев весь период времени, предшествующий году
. Рассмотрев весь период времени, предшествующий году 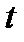 , получим следующую формулу для фондов, входящих в строй в этом году:
, получим следующую формулу для фондов, входящих в строй в этом году: 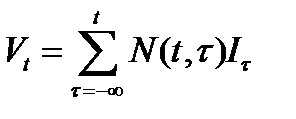 . Тогда уравнение движения фондов будет иметь вид
. Тогда уравнение движения фондов будет иметь вид 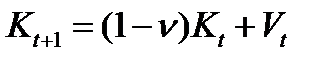 .
.
Непрерывным аналогом этих соотношений будут, соответственно, следующие формулы:
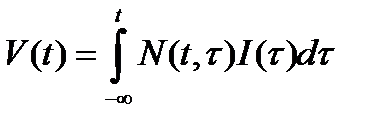 (1)
(1)
 (2)
(2)
Величина 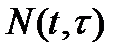 показывает, какая доля инвестиций, сделанных в момент
показывает, какая доля инвестиций, сделанных в момент 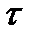 , будет освоена в момент
, будет освоена в момент 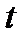 . Если эта доля зависит лишь от длительности
. Если эта доля зависит лишь от длительности 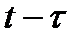 промежутка освоения, то говорят о стационарности процесса ввода инвестиций в действие. В этом случае
промежутка освоения, то говорят о стационарности процесса ввода инвестиций в действие. В этом случае 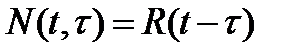 , где
, где 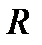 - некоторая функция одной переменной. Тогда формула (1) принимает вид
- некоторая функция одной переменной. Тогда формула (1) принимает вид
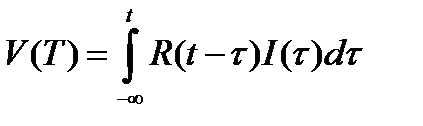 .
.
Вводя новую переменную 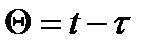 , получим:
, получим:
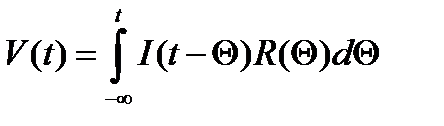 (3)
(3)
Остановимся на условиях, которым должна удовлетворять функция 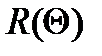 . Естественным выглядит предположение о том, что доля сделанных в момент
. Естественным выглядит предположение о том, что доля сделанных в момент 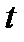 инвестиций, которая будет освоена в момент
инвестиций, которая будет освоена в момент 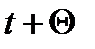 , тем меньше, чем больше
, тем меньше, чем больше  . Это означает, что функция
. Это означает, что функция 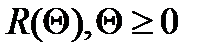 должна быть убывающей или, по крайней мере, невозрастающей. При больших
должна быть убывающей или, по крайней мере, невозрастающей. При больших  значения
значения 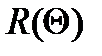 должны быть близки к нулю. Это условие можно формализовать следующим образом:
должны быть близки к нулю. Это условие можно формализовать следующим образом: 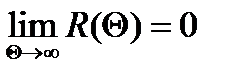 (4)
(4)
Понятно, что при равномерных капиталовложениях ( 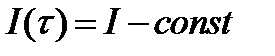 ) фонды будут входить в строй также равномерно:
) фонды будут входить в строй также равномерно: 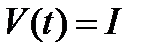 . Тогда из (3) получаем:
. Тогда из (3) получаем:
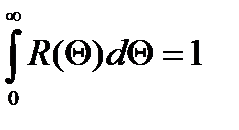 .
.
Легко убедиться в том, что перечисленным условиям удовлетворяет функция 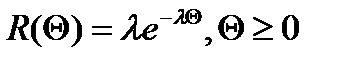 (5), где
(5), где 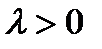 которое довольно часто используется при математическом моделировании процессов освоения капиталовложений.
которое довольно часто используется при математическом моделировании процессов освоения капиталовложений.
Вычисляя производную правой части (3) по правилам дифференцирования несобственных интегралов по параметру, получим
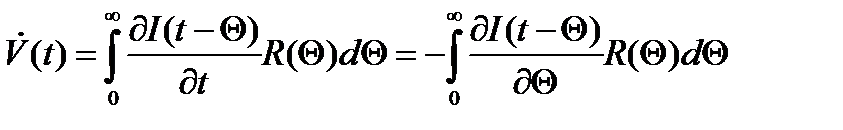
Интегрируя последний интеграл по частям с учётом (4) будем иметь
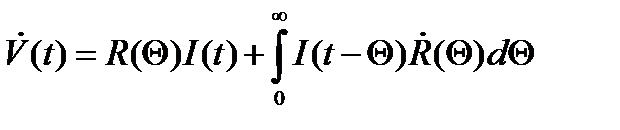 (6)
(6)
Для экспоненциального закона запаздывания (5) 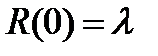 ,
, 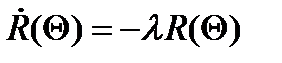 . В этом случае соотношение (6) принимает вид
. В этом случае соотношение (6) принимает вид
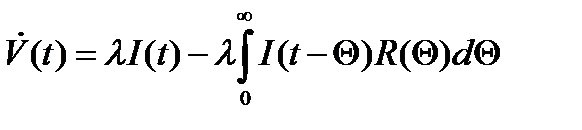 .
.
Отсюда и из (3) получаем
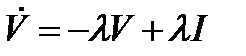 (7)
(7)
Таким образом, в случае экспоненциального закона запаздывания объём вводимых в действие фондов может быть найден как решение обыкновенного дифференциального уравнения (7). При этом необходимо задать капиталовложения 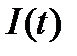 как функцию времени и начальные значения
как функцию времени и начальные значения 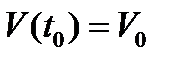
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|